Expressions, formulas and substitution
Year level: 7
Strand: Algebra
Lesson length: 60 mins
In this lesson, students build on their understanding of algebraic expressions. Explore substituting values into formulas to determine unknowns using a variety of contexts to reinforce the importance of algebra in real life.
This is the second lesson in a series of lessons to develop understandings and proficiency in algebraic thinking.
Curriculum information
Achievement standard
Students use algebraic expressions to represent situations, describe the relationships between variables from authentic data and substitute values into formulas to determine unknown values.
Content descriptions
Students recognise and use variables to represent everyday formulas algebraically and substitute values into formulas to determine an unknown. AC9M7A01
Students formulate algebraic expressions using constants, variables, operations and brackets. AC9M7A02
General capabilities
Numeracy:
- Number patterns and algebraic thinking (Level 6)
Critical and creative Thinking:
- Interpret concepts and problems (Level 5)
Assessment
Use the following formative assessment to gauge where students are at.
Exit ticket questions:
- If x = 2, find the value of 2x–9
- Label the parts of this expression: 3x–2
- In your own words, what is the difference between an expression and an equation?
Areas of challenge
Some students may:
- think that the '=' sign indicates an example, rather than expressing an equivalence relationship
- think that a variable represents the count for the number of objects (for example, 3a means 3 apples)
- have difficulties understanding the lack of multiplication signs in algebraic expressions, such as 3 x a = 3a
- have difficulties with different decimal and fraction representations in algebraic expressions, such as 0.5a = 1 2 a = a 2
- think that a particular variable always holds the same value
- think that the same variable in an expression can hold different values, such as thinking that t could be 2 and 4 in the expression t + t = 6.
Prerequisite student knowledge and language
Prior to this lesson, it is assumed that students have knowledge of:
- the concept of variables
- constructing algebraic expressions from word problems
- conventions associated with the order of operations for integers
- knowledge of algebraic conventions (covered in prior lesson)
- how ‘=’ indicates an equivalence statement
- what is meant by an expression (from prior lesson)
- how to measure length accurately using rulers (to the mm)
- how to use formulas to find the area of a triangle and rectangle
- decimal notation and rounding decimals
- using calculators to carry simple calculations
- how to measure mass in grams.
What you need:
Lesson plan (Word)
Teacher's slides (PowerPoint)
Warm up with algebraic expressions worksheet (Word)
Workstation instructions (Word)
Stacking cups and two different coloured counters, kitchen scale, rulers and calculators
Learning goals
Learning intention
- We are learning to match word problems to their algebraic expression.
- We are learning to understand the difference between an expression and a formula and learn algebra terminology such as constant, coefficient, variable and operator.
- We will substitute values into equations in a range of scenarios.
Success criteria
By the end of the lesson, students can:
- explain the difference between a variable and an expression
- identity a variable, coefficient, constant and operator
- substitute values into a range of equations in a range of scenarios.
Why are we learning about this?
Equations are useful in many everyday life scenarios – including representing our wages – or in formulas for finding the area of a shape or the density or volume of an object. Substituting values into equations allows us to easily explore a range of phenomena in the real world and solve a wide variety of problems.
Learning hook 15 mins
To start
Print the Warm up with algebraic expressions worksheet (one per student) and access the downloadable teacher’s slides to present this lesson. Have students complete the worksheet individually. Once complete, students can swap worksheets with a partner and compare answers. Take note of discussions between pairs and use this time to note misconceptions or concepts requiring more attention.
Introduce new concepts
- Use slides 1 and 2 and refer to teaching notes provided with the slides to introduce students to the learning intentions of the lesson. Remind them to think back to what was learnt about constructing algebraic expressions. Explicitly explain you will be continuing to construct algebraic expressions and will be working with algebraic equations and substituting values to find and unknown (slides 3–5). As the term ‘equation’ is being introduced, explain to students the difference between equations and expressions, and discuss key terminology associated with expressions.
- Show students the following example:
‘Mark gets $3 less pocket money a week than his older brother Sam.’
With the class, construct an equation that represents the scenario and use cups and counters to model this equation (slides 6 and 7). Explain to students that if we have an algebraic equation and we are told the value of an unknown, we can substitute this value into the equation. Use the example from above, substituting in that Sam gets $5 each week. Model the process of substituting in $5 for S by filling the cup with 5 counters. Show students how the value of the counters in the cup (+5) and the –3 equate to an answer of $2. Explain to students that in the question we have substituted S for 5 and that in algebra substitution this means replacing a variable with a particular value.
- Go to slides 8 and 9 to conduct another whole-class example of substitution using cups and counters using the following ‘Taj has several books. Lulu has twice as many. Construct an expression to show how many books Lulu has. If Taj has 6 books, how many does Lulu have?’
- Now work through another whole-class example without concrete materials (slides 10 and 11): ‘Roshini has a little brother, Rami. If you double Rami’s age and add 3 more years, you get Roshini’s age. If Rami is 3, how old is Roshini?’
Explore 35 mins
Enable students to explore the concept
Download and print the Workstation instructions to be displayed on tables for students to rotate through. Pre-cut the triangles and shapes ready to go. Arrange students in groups of three or four at each workstation. Allow students to engage in each task for 15 minutes, then rotate.
Workstation 1: Students measure the dimensions of a variety of cut-out rectangles and triangles using rulers. Using the formulas for the area of a triangle and area of a rectangle, students substitute measurements into the formula to calculate the area of each shape.
Workstation 2: Students measure the mass of various objects using kitchen scales. Using the formula for density, and each objects’ approximated volume, students calculate the density of each object and order them from least to most dense.
Workstation 3: Students consider a wage scenario and, with scaffolding, construct the algebraic equation to represent the total wages earnt each week. From this equation, students answer various salary questions to eventually determine Milly’s annual salary.
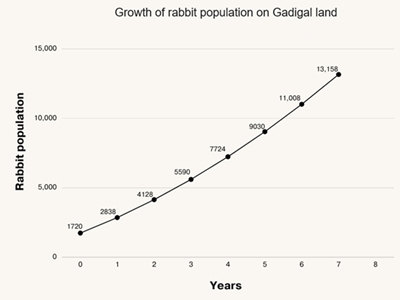
Workstation 4: Students consider the given graph and scenario: growth of a rabbit population on Gadigal land in NSW. In this scenario, students use the given equation that models the graph to extrapolate expected values for the rabbit population and will answer a set of given questions for the scenario.
Differentiation (all abilities): Each workstation has three differentiated levels of challenge: ‘mild’, ‘medium’ and ‘spicy’. Allow groups to choose the difficulty level at each workstation. It is encouraged that students work in mixed-ability groups to support effective collaborative learning.
For further reading go to: The spread of rabbits throughout Australia.
Summary and reflection 10 mins
In groups, pairs or individually, students can conclude the lesson by attempting the GeoGebra lesson Substituting and evaluating expressions.