Year level: 2

Strand: Algebra

Lesson length: 60 mins

Use this lesson to explore and record additive patterns through classroom discussion. Organise mathematical observations in a table to more easily identify patterns. 

Recording additive patterns Image

Achievement standard

Students describe and continue additive patterns that increase and decrease by a constant amount and identify missing elements in the pattern.

Content descriptions

Students recognise, describe and create additive patterns that increase or decrease by a constant amount, using numbers, shapes and objects, and identify missing elements in the pattern. AC9M2A01

General capabilities

Numeracy

  • Additive strategies (Level 7)
  • Number patterns and algebraic thinking (Level 3)

Assess students' proficiency in recognising and extending an additive pattern.

Ask students to:

  1. Think of an additive pattern.
  2. Describe the pattern.
  3. Identify the next step in the pattern, by referring to the previous step.

Differentiation (support)

For students building their confidence, allow them to use physical materials to describe the pattern.

Some students may:

  • not yet recognise the additive pattern, particularly if they are unfamiliar with skip counting by 3s
  • have difficulty organising their observations in the table and relating position to the number of blocks
  • need support to extend the pattern and predict the number of blocks that comes next.

It is expected that students have:

  • knowledge of counting by 2s, as the number of blocks increases by 2 in each position
  • experience identifying and extending simple numerical or visual patterns
  • basic addition, especially the idea of repeated addition (for example, adding 2 each time)
  • familiarity with reading and completing simple tables, where they can relate one set of numbers to another (for example, position and number of blocks).

It is also assumed that students are familiar with terms such as:

  • pattern
  • step (for example, in a process)
  • position
  • representation (such as a drawing)
  • table (to organise data).

What you need:

Learning goals

Learning intention

  • We are learning to explore visual patterns using blocks to understand and extend additive sequences.
  • We are learning how to organise our mathematical observations in a table and use reasoning to predict the next steps in the pattern.

Success criteria

By the end of this lesson, students can:

  • identify the pattern in the number of blocks at each position
  • extend the pattern by predicting the number of blocks
  • organise observations in a table
  • explain the rule for the pattern
  • draw a visual representation of the blocks at each position.

Why are we learning about this?

Visual patterns offer students an engaging way to explore early algebraic concepts. They encourage reasoning and problem-solving, while also helping students develop their own methods for recording and understanding additive patterns. By using tables to organise mathematical observations, students can see how structured thinking supports clear and logical problem-solving.

Learning hook 10 mins

  • Use the teacher’s slides to introduce this part of the lesson.

Refer to slide 2 to introduce the task.

Ask students: ‘What do you notice? What do you wonder?’ about the visual pattern made by the arrangement of four blocks displayed on the slide.

Slide with text What do you notice? What do you wonder? Under text shows four purple toy blocks on a wooden surface. The first block consists of 2 smaller blocks stacked together, the second has 4 blocks, the third is made of 6 blocks, and the last block is composed of 8 blocks.

Slide 2

Use a classroom talk to generate discussion about the arrangement of the blocks. Provide 15 to 30 seconds of think time. During this time, students refrain from raising their hand when they have an idea. Instead, they look and think for the entire time and see how many ideas they can come up with.

List what students notice or wonder. Refer to the notes on slide 2 for examples to use as prompts or to guide further discussion.

Explore 40 mins

Introduction: repeated patterns (10 mins)

Use the arrangement of blocks on slide 3 to illustrate a repeating pattern. Talk through the arrangement. Introduce the term ‘step’ to describe the position of the arrangements. Ask: ‘What is the difference in blocks from one step to the next? How is the number of blocks increasing from one step to the next?’ Ask them to predict the next step of the pattern. Ask: ‘How did you know what it would be?’

Slide with text Can you see pattern? Under text shows four purple toy blocks on a wooden surface. The first block consists of 2 smaller blocks stacked together, the second has 4 blocks, the third is made of 6 blocks, and the last block is composed of 8 blocks.

Slide 3

Use slides 4, 5 and 6 to discuss the pattern and extend the pattern to positions 5 and 6. Students should be able to recognise the pattern of increasing by two each position. Ask: ‘Who can tell me how many blocks will be in position 5?’ Ask them to explain how they worked it out.

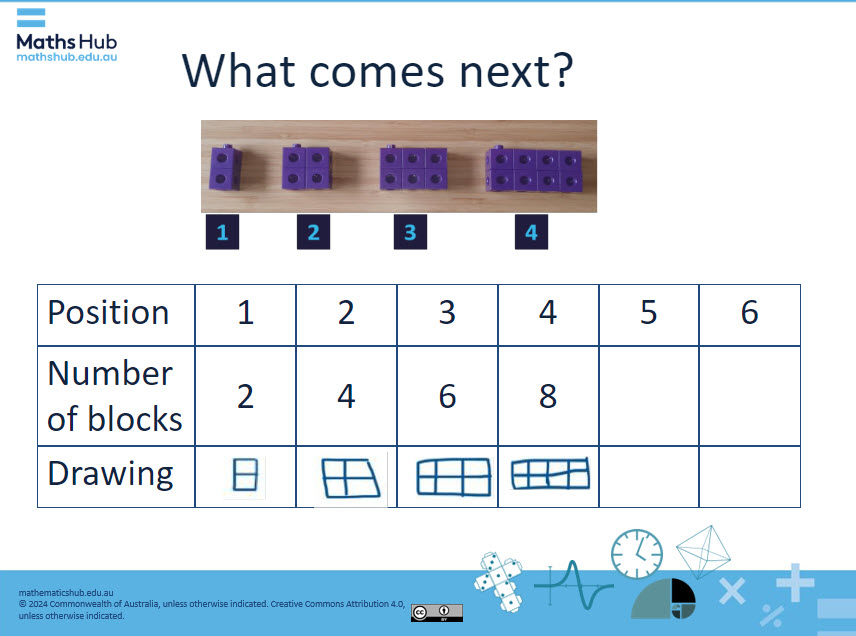
Slide with text What comes nest? Under text shows four purple toy blocks on a wooden surface. The first block consists of 2 smaller blocks stacked together, the second has 4 blocks, the third is made of 6 blocks, and the last block is composed of 8 blocks. A table is under the arrangement of blocks to record pattern.

Slide 4

Activity 1: Complete the pattern (15 mins)

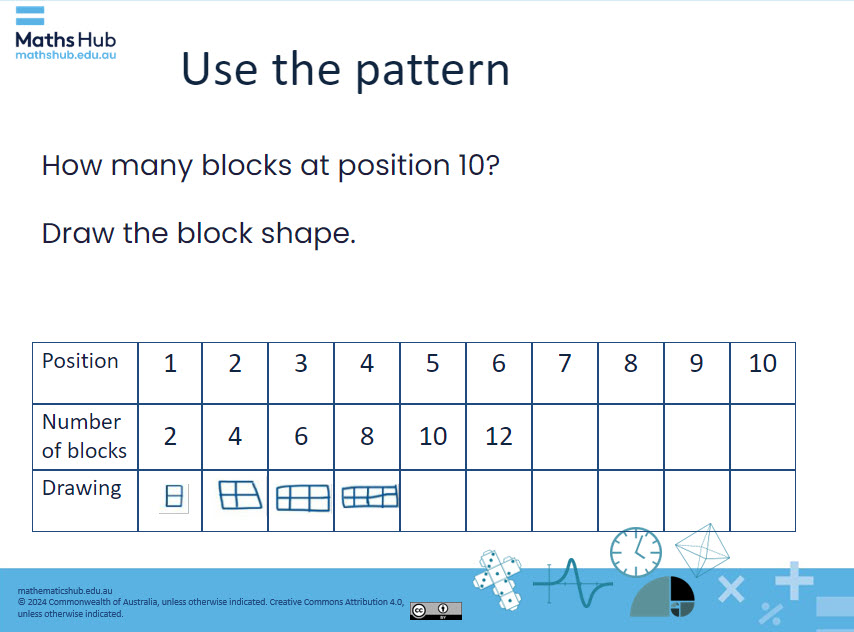
A table to record pattern. The table includes position number 1 to 10, number of blocks, 2, 4, 6, 8 and a drawing of each block in each column.

Slide 7

Engage students in completing the pattern by creating a table to record their ideas.

  • Ask: ‘How many blocks will there be at position 10?’
  • Encourage students to think about how the pattern increases by 2 blocks at each step.
  • Roam the room and use questioning to assess their understanding of this additive pattern.
  • Share completed tables and review the additive pattern.

Differentiation (support):

  • What comes next in position 7 if it’s 2 more than position 6?
  • What blocks come after position 7? How do you know?

Differentiation (extension):

  • Can you work out the number of blocks at positions like 20, 50 or even 100?
  • How did you calculate the number of blocks at those positions?
  • If you had 100 blocks, how far could you extend the pattern?

Activity 2: Represent an additive pattern (adding 3 each time) (15 mins)

Slide with text What do you notice? What do you wonder? Under text shows four purple toy blocks on a wooden surface. The first block consists of 3 smaller blocks stacked together, the second has 6 blocks, and the last block is composed of 9 blocks.

Slide 8

Introduce another additive pattern, this time one that increases by 3 each step.

Use slides 9 and 10 to set up the challenge of working out how many blocks there will be at position 10 using this pattern.

Engage students in completing the pattern by creating a table to record their ideas.

  • Ask: ‘How many blocks will there be at position 10?’
  • Use questioning to prompt them to consider how the pattern increases by 3 blocks for each position.
  • Roam the room and use questioning to assess their understanding of this additive pattern.
  • Share completed tables and review the additive pattern.

Differentiation (support)

  • For students building their confidence, complete the pattern for fewer positions.

Differentiation (extension)

  • For students ready for a challenge, ask them to consider what the pattern would look like in reverse. Pose the question: ‘If we start at position 10 and subtract 3 blocks at each step, what does the arrangement look like?

Summary and reflection 10 mins

Summarise the lesson’s key points and invite students to reflect on what they’ve learned:

  • What strategies did you use to identify and extend the additive patterns in both activities? How did those strategies help you find the number of blocks at different positions?
  • How did working with tables improve your understanding of the patterns? What did you find most helpful or challenging about this method?
  • Can you think of where you have seen additive patterns in your daily life?