Using algebra tiles to solve equations
Year level: 7
Strand: Algebra / Measurement
Lesson length: 60 mins
In this lesson, students use algebra tiles to solve one-variable linear equations involving multiplication and division, applying these skills in real-world contexts to enhance their understanding.
This is the fourth lesson in a series of lessons to develop understandings and proficiency in algebraic thinking.
Curriculum information
Achievement standard
Students use algebraic expressions to represent situations, describe the relationships between variables from authentic data and substitute values into formulas to determine unknown values. They solve linear equations with natural number solutions.
Students use formulas for the areas of triangles and parallelograms and the volumes of rectangular and triangular prisms to solve problems.
Content descriptions
Students solve one-variable linear equations with natural number solutions; verify the solution by substitution. AC9M7A03
Students solve problems involving the area of triangles and parallelograms using established formulas and appropriate units. AC9M7M01
General capabilities
Numeracy
- Number patterns and algebraic thinking (Level 6)
Critical and Creative Thinking
- Interpret concepts and problems (Level 5)
Assessment
The following formative assessment activity is recommended as the conclusion of this lesson.
- Students complete the Algebra maze individually, which is found in the Solving equations shapes worksheet.
- Evaluate students’ responses to the formative assessment to determine their conceptual understanding and procedural fluency with the topic.
- Consider incorrect responses on the maze to determine underlying misconceptions.
Prerequisite student knowledge and language
Prior to this lesson, it is assumed that students have knowledge of:
- the concept of variables
- constructing equations from word problems
- conventions associated with the order of operations for integers
- knowledge of algebraic conventions (covered in prior lessons)
- how ‘=’ indicates an equivalence statement
- how to substitute values into equations
- how to solve one-variable linear equations involving addition and subtraction
- how to use formulas to find the area of a triangle, rectangle and parallelogram.
As this lesson will be using two different coloured algebra tiles to denote positive and negative values, it is important that prior to this lesson, students have practised using concrete tools to carry out calculations involving positive and negative numbers.
Areas of challenge
Some students may:
- think that the ‘=’ sign indicates to record an example, rather than expressing an equivalence relationship
- think that a particular variable always holds the same value
- find identifying inverse integer operations counterintuitive, particularly when negative integers are involved
- forget, or not realise, that they need to do the same thing to both sides of the equation
- have trouble neatly recording each step of their working out when solving equations.
What you need:
Lesson plan (Word)
Teacher's slides (PowerPoint)
Solving equations shapes worksheet (Word)
Algebra mats and algebra tiles (PDF)
Learning goals
Learning intention
- We are learning to construct equations for given word problems.
- We will substitute values into equations.
- We will solve equations involving multiplication and division.
- We will use algebra to find unknown lengths and areas for various shapes.
Success criteria
By the end of the lesson, students can:
- solve one-step equations involving addition, subtraction, multiplication and division with and without concrete materials
- recognise the algebra required to solve geometric problems for various shapes and solve them.
Why are we learning about this?
Equations are useful in many everyday scenarios, including representing our wages, or formulas for finding the area of a shape or the density or volume of an object. Substituting values into equations allows us to easily explore a range of phenomena in the real world and solve a wide variety of problems.
Learning hook 20 mins
Note: the teacher’s slides are designed to complement the teaching of this lesson. The teaching notes with the slides also provide the instructions as you progress through the lesson.
Introduction:
Connect to prior learning
- To begin, explain to students that they will solve interactive mobile puzzles using digital algebra tiles. Provide the website address, https://solveme.edc.org, which is shown on slide 2, and explain to students how to begin. Ask them to select ‘mobiles’ then ‘play’ and start at Explorer puzzle 1 to prime algebraic thinking ready for the lesson.
Differentiation: Students can complete as many puzzles as they like, allowing for differentiation. Students can choose more difficult puzzles if needed, rather than beginning at puzzle 1. Allow students to work in pairs if they find the puzzles challenging.
Learning hook
- Introduce students to the specific learning intentions of the lesson also found on slide 2. Use slides 3 and 4 to review solving equations that involve addition and subtraction.
Differentiation (enable): Students can think-pair-share their responses to the questions on slides 3 and 4, allowing for collaborative learning. Find the lesson: Solving equations with algebra mats with addition and subtraction.
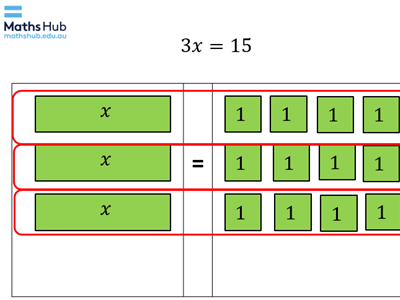
- Introduce students to solving equations using algebra tiles (slides 5–11). The slides are animated and with each click the next step is revealed, allowing you to progressively go through each slide without revealing the next step so soon. This allows for explicit explanation, iterations, analogies and further explanations for all the class.
Differentiation: Give pairs of students a set of algebra tiles and an algebra mat (also known as an equation mat) so that they can model each example question along with the teacher.
Explore 30 mins
Note: download and print the Algebra tiles and algebra mats PDF and laminate them if you can. You need enough for half the class as students work in pairs. You will need to cut them, or have students do this. Also print out the Shapes worksheet for your class, one per student, even though students remain working in pairs.
Explore and Investigate
Model solving equations using digital algebra tiles (Mathigon and Tutorial) or download the Algebra mats and Algebra tiles for a hands-on experience. Show students how they should structure their written solutions for the question.
Activity 1:
In pairs, allow students to solve questions generated on Mathigon as shown by you previously. If possible, instruct one student to model the problem using digital algebra tiles, and the other student to model the same problem using the physical algebra tiles and equations mat. Both students record the steps for solving the equation in their exercise books. Pairs can swap using the digital or physical algebra tiles.
Iterate by using only concrete Algebra tiles whereby students can swap and explain their thinking to reach the solution.
Activity 2:
In pairs, students complete the Solving equations shapes worksheet. Note that Algebra maze in the final pages are recommended as an assessment opportunity.
Differentiation: Pairs who complete the questions early can create their own area puzzles and swap with their partner.
Summary and reflection 10 mins
Come together as a class.
- Facilitate discussion on the learning successes.
- Try to address misconceptions that may be raised.
- Ask whether anyone had any different strategies they used or ways of thinking to solve the problems. Have them come up to the whiteboard to demonstrate.
- Note those students who need extra clarification and practice.
- Note those students who may wish to expand their learning.
- Connect the abstract ideas with real-world examples; have students call out examples.
- Create channels for students to come to you individually with confusions.