Teaching strategies
Six key principles for effective teaching of mathematics are outlined in Peter Sullivan’s Teaching Mathematics: Using research-informed strategies (2011). These principles draw on work from a range of researchers in this field, including Good, Grouws and Ebmeier (1983); Hattie (2009); Swan (2005); Clarke and Clarke (2004); and Anthony and Walshaw (2009).
The six principles are articulating goals, making connections, fostering engagement, differentiating challenges, structuring lessons, and promoting fluency and transfer. Explore teaching strategies aligned to the principles below.
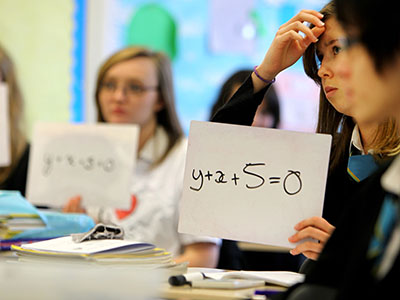
Principle 1: Articulating goals
Identify key ideas that underpin the concepts you are seeking to teach, communicate to students that these are the goals of the teaching, and explain to them how you hope they will learn (Sullivan, 2011).
Setting goals
Having a clear learning goal when planning a lesson or sequence of lessons ensures that learning activities are targeted towards the goal.
Read morePrinciple 2: Making connections
Build on what students know, mathematically and experientially, including creating and connecting students with stories that both contextualise and establish a rationale for the learning (Sullivan, 2011).
Culturally responsive pedagogies
Mathematics is not an exclusive western construct. Therefore, it is important to acknowledge and demonstrate the mathematics to be found in all cultures.
Read more
Gender-inclusive maths
It is well known that girls tend to be under-represented in higher level mathematics classes. How teachers talk and interact with their students is key to overcoming this.
Read more-
![Mathematics investigation Image]()
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Read more -
![Using games and storybooks Image]()
Using games and storybooks
Games and storybooks are great resources to use in the classroom and are engaging for students.
Read more -
![Classroom talks Image]()
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Read more -
![Concrete, Representational, Abstract (CRA) Image]()
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Read more -
![Worked examples Image]()
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Read more
-
![Targeted teaching Image]()
Targeted teaching
Targeted teaching involves the use of assessment data to target interventions to small groups or individual students.
Read more -
![Differentiated teaching Image]()
Differentiated teaching
Differentiation involves teachers creating lessons that are accessible and challenging for all students.
Read more -
![Questioning Image]()
Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Read more -
![Feedback Image]()
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Read more -
![Collaborative learning Image]()
Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Read more
-
![Structuring lessons Image]()
Structuring lessons
A well-developed lesson structure is important for both teacher and students.
Read more -
![Explicit teaching Image]()
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Read more -
![Multiple exposures Image]()
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Read more -
![Universal Design for Learning (UDL) Image]()
Universal Design for Learning (UDL)
Universal Design for Learning (UDL) encourages teachers to design their lessons with all their learners in mind from the beginning.
Read more
Principle 6: Promoting fluency and transfer
Fluency is important, and it can be developed in two ways: by short everyday practice of mental processes; and by practice, reinforcement and prompting transfer of learnt skills (Sullivan, 2011).
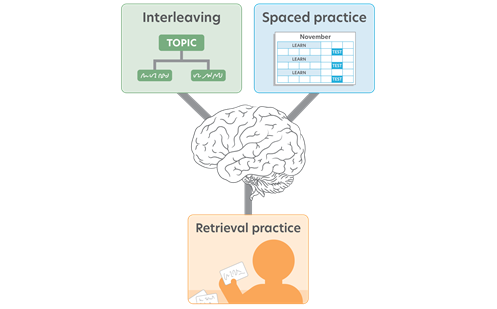
Spaced, interleaved and retrieval practice
These are three strategies that can be used to increase student retention and recall of their learning.
Read more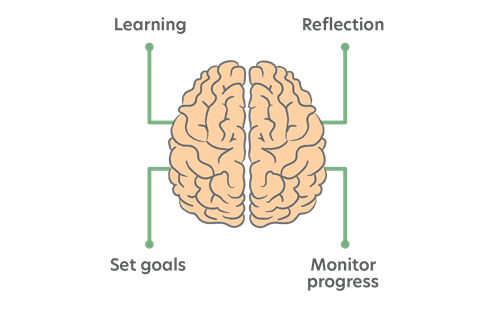
Metacognitive strategies
Metacognitive skills are those that students need to be able to reflect on their own learning, set goals for themselves, monitor their progress and make improvements to move forward.
Read more