Planning tool

Students:

• apply linear, quadratic and exponential functions to modelling contexts and state their reasons for selecting a particular model
• use tables of values to look for patterns in their data, recognising that linear functions have constant first differences, quadratic functions have constant second differences and exponential functions have a constant ratio between consecutive values of the dependent variable
• work with authentic information, data and situations to translate real-life contexts into mathematical models and appreciate that these models are often approximations of the actual situation
• use mathematical-modelling approaches to solve authentic and real-world problems involving variables that show growth or decay, for example, financial contexts
• create a report that outlines the problem and the modelling used, and explains methods, assumptions, limitations and findings
• communicate their model and findings to their peers and teacher, and respond to feedback to refine their model.

Some students may:

• not appreciate that a model is a representation of relationships between variables and is based on a set of assumptions, and that it often provides an approximation.
• not identify suitable independent and dependent variables to model the situation.
• not recognise that a model has limitations, for example, it applies to a given set of values and may not be able to be extrapolated beyond these.
• need further guidance with conceptual understanding of a https://nrich.maths.org/8336problem, procedural understanding and mathematical reasoning.
• not sufficiently recognise the importance to the modelling process of being able to clearly interpret and communicate the application of a model, and refine it based on critical feedback from others.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention 

• We are learning to apply knowledge of the properties of linear, quadratic and exponential functions and the differences between them, when selecting a function to model given data.
• We are learning to model depreciation using an exponential decay model.

Why are we learning about this? 

Modelling real-life contexts using mathematical functions allows us to better understand a situation, make informed decisions, explore alternative scenarios and consider future possibilities.  

What to do 

Deciding which model to use

Imagine you had some data you wanted to model. How would you know whether to use a linear, quadratic or exponential function for this model? Understanding the characteristics and features of each of these functions is important to help you decide.

1. Write down your understanding of the properties and features of each of the three functions: linear, quadratic and exponential.
2. Graph each of the following three functions using a graphics calculator or an online graphing program such as GeoGebra.
   linear: y = 2x     quadratic: y = x²    exponential: y = 2^x 
3. Reread your response to step 1 and refine as needed.
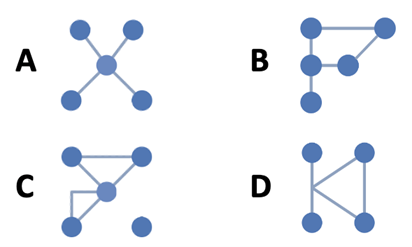
4. Four data sets of points are given below: A, B, C and D. Decide which type of function you would use to model each one: linear, quadratic or exponential. Explain your choice.

Modelling depreciation

1. A new printing machine is bought for $8000. Its value depreciates (decreases) by 15% every year.
2. How much is the printing machine worth at the end of the first year? (Hint: it’s much more than $1200.)
3. By the end of the second year, the printing machine will lose 15% of its ‘end of 1st year’ value. How much is it worth at the end of the 2nd year?
4. By the end of the third year, the printing machine will lose 15% of its ‘end of 2nd year’ value. How much is it worth at the end of the 3rd year?
5. Which one of the following rules models the depreciation of the printing machine, where V represents its value in dollars and y represents years after purchase.
   • V = 0.15^y
   • V = 0.85^y
   • V = 8000(0.85)^y
   • V = 8000(0.15)^y
6. To check your answer, graph the rule you believe is correct in using graphing software, and check if it corresponds to your answers from steps 1 to 3.
7. Use graphing software to graph the correct exponential model from step 4 and the linear function
   ­y = –0.85x + 8000. Comment on the differences between linear and exponential models for depreciation.

Additional information and practice

Nrich: Investigating epidemics

Success criteria 

• I can apply knowledge of the properties of linear, quadratic and exponential functions and the differences between them, to select a suitable function to model given data.
• I can model depreciation using exponential decay.