Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10SP02
Numeracy Progression: n/a
At this level, students develop the ability to use visual representations to solve problems. Networks is a new area for Year 10 and may be unfamiliar to many teachers. Also called 'graph theory', networks and network diagrams are ways of displaying and describing relationships and modelling connections. Networks serve as a model for decision making, much like a flowchart, and enable users to follow a sequence of tasks that show clear connections between them.
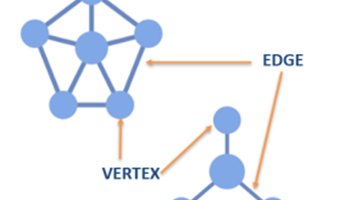
It’s important to demonstrate how networks work and how they apply in the real world. Ensure students are introduced to common vocabulary such as 'nodes', 'vertices' and 'edges', and use these terms when they are working and describing. It is important to emphasise that the order of events is important so that a pathway may be taken, and that the diagram is not just a set of visual of nodes that are unrelated. Spend time on the elements of networks and how to draw them, so that students may equally interpret a diagram when they are presented with one.
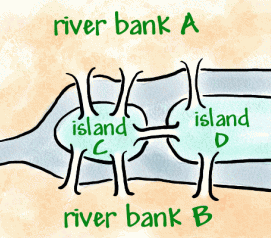
Networks may be drawn by hand in order to understand and design them, but appropriate dynamic geometric software can add complexity and engagement as students make sense of the topic. Furthermore, engagement may be enhanced by talking about the Konigsberg problem alongside referencing the application in the real world; for example, social networking, electrical diagrams and travel.
Teaching and learning summary:
- Demonstrate how to draw a network diagram.
- Use the bridges of Konigsberg problem as an example.
- Discuss Euler’s formula: F + V = E + 2.
- Introduce the terminology of networks:
- node (or vertex) – a point, which could be a person, place, activity
- edge (or arc) – this is a line joining nodes, which could represent a route, cost, activity
- degree – the number of edges at a node
- weight – this represents the cost of using the edge
- graph – a group of nodes and edges.
- Investigate where networks can be used to model authentic situations – travel, social networks, electrical diagrams, distribution.
Students:
- can draw a diagram to model a network
- understand and use the terminology of networks
- interpret networks and network diagrams modelling relationships and connectedness
- know where networks can be used to model authentic situations.
Some students may:
- have difficulty constructing a network diagram that is based on a sequenced set of events
- assume that a pathway may only go in one direction when some pathways go backwards, which leads to misinterpreting a network diagram.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to think about networks as a sequence to follow.
- We are thinking about networks as a series of connections.
Why are we learning about this?
Giving instructions can be complex and sometimes involves many interrelated connections. Sometimes we need to give complex instructions to others, machines, software programs or mapping programs so that the sequence and connections are recorded, and can be followed or checked or provide a way of understanding in our complex world.
What to do
Below are two resources for you to learn more with your family. The first is an explanatory resource that helps you figure out what basic networks encompass.
The second resource is an interactive you can use on your device. The great thing about interactives is that you are more engaged with learning, can re-do it continually, connect what you have just learnt and experience how it works.
Basic network
- Read through this resource , which gives a simple, clear explanation of nodes, edges and weights.
- Make a mini-notebook to use use as a reference guide so that each page is a new term, definition and explanation. Give examples where you can.
Moving through a network
3. Use the interactive to take learning further by demonstrating differences between paths, walks, trials and circuits.
Success criteria
- I can understand networks and use the right vocabulary.
- I can make or follow pathways and see how a complex system is connected and interconnected.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Mathematics investigation
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Explicit teaching
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
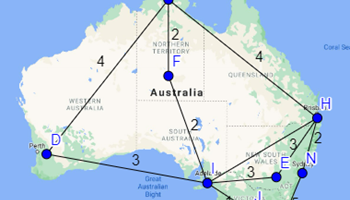
Capital Airways: Part 1
In this lesson students are introduced to the concept of a network through an airline route map.
Go to resource -
Capital Airways: Part 2
In this lesson students use mathematical modelling to re-design the network map of the airline route to improve the airline’s profitability.
Go to resource -
Basic network
This resource gives a simple, clear explanation of nodes, edges and weights.
Go to resource -
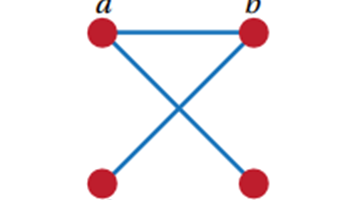
Graph theory
In this resource, students and teachers work through the basics of graph theory, with examples and questions for practice.
Go to resource -
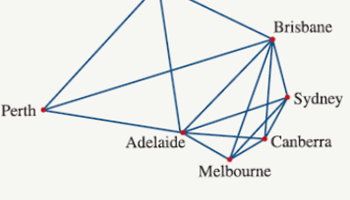
Moving through a network
This resource explains some of the basics of network theory.
Go to resource
Assessment
By the end of Year 10, students can interpret networks used to represent practical situations and describe connectedness.
-
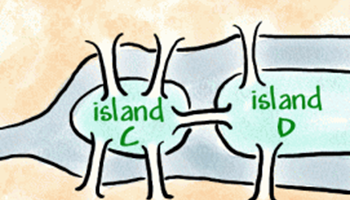
The bridges of Konigsberg
Is it possible to go for a walk around Konigsberg, crossing each bridge exactly once? Students use their knowledge of networks to complete a series of questions on this problem.
Go to resource -
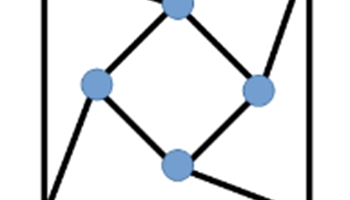
Can you traverse it?
Print this worksheet and have students practise their spatial thinking to solve transversing network diagrams.
Go to resource