Efficient strategies: Year 5: Planning tool

Expected level of development

Australian Curriculum Mathematics V9: AC9M5N06, AC9M5N07

Numeracy Progression: Interpreting fractions: P8, Multiplicative strategies: P7

At this level, students learn efficient ways to multiply and divide numbers using increasingly sophisticated strategies. They develop flexible strategies to solve multiplication facts and related division facts and consolidate automatic recall. They identify and describe factors and multiples of whole numbers and use them to solve problems.

Use classroom talks to help students work collaboratively to build their strategies to solve multiplication problems.

Show how a doubling strategy can simplify a multiplication problem.
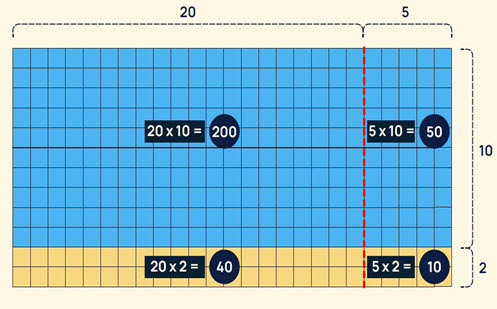
Model place value partitioning strategies to multiply larger numbers by one-digit and two-digit numbers. For example, to multiply 24 x 12, first multiply 10 x 24 and then multiply 2 x 24 and add the two products together. Use area models and arrays to show partitioning.
Make explicit how factors can be used to simplify calculations. For example, 15 x 16 can be simplified into 5 x 3 x 4 x 4 and rearranged to 5 x 4 x 3 x 4 = 240 to make the calculation easier. The rearranging of these numbers contextualises the commutative and distributive properties of multiplication.

Provide opportunities to solve division problems presented as number stories in familiar contexts. Where there is a remainder, have students interpret the meaning and represent the problem. Discuss the situations where a remainder needs to be rounded, for example, when dealing with passenger numbers on a train.

Encourage students to solve simple division problems mentally drawing on the known multiplication facts. For example, when given the problem of sharing 36 stickers between 9 people, students see the problem as 36 divided by 9 and use their times table facts of 9 x 4 = 36 to work out how many 9s make 36.

Teaching and learning summary:

Develop efficient strategies for multiplying and dividing numbers.
Connect concrete, visual and abstract representations of multiplicative situations using familiar contexts.
Interpret and represent the remainder in division calculations.

Students:

solve problems involving multiplication of large numbers by one-digit or two-digit numbers using efficient mental strategies, written strategies and appropriate digital technologies
solve problems involving division by a one-digit number, including those that result in a remainder
identify and describe factors and multiples of whole numbers and use them to solve problems.

Some students may:

say ‘3 into 15’ to solve the division problem, which may indicate they have limited understanding of the meaning of division
have little understanding of what the remainder represents
have difficulty matching materials and representations to number problems
get confused when a division answer includes a zero, for example, when dividing 6,540 by 5, they don’t record 0 as it means nothing so write the answer as 138 instead of 1,308.

To address these problems, use classroom talks to show different representations of division, using correct terminology when discussing division problems, and using efficient strategies to solve the problems. Discuss problems with and without remainders and use examples to show what the remainder means.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

We are learning that division is the ‘sharing’ of items, and that sometimes division can result in remainders if the items can’t be evenly shared.

Why are we learning about this?

Being able to fluently divide numbers and explain my thinking builds number sense and is helpful when solving more complex problems.

What to do

Open the link to the Remainders game.
Watch the video to learn how to play the game.
Collect the resources listed below the video. Note: if you don’t have counters, find 24 objects that are the same items, for example, paperclips or pasta shells.
Play the game with a friend or family member.

Success criteria

I can:

solve problems involving division and explain my thinking.

Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.

Planning tool

Year levels

Strands

Topics