Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M5N01
Numeracy Progression: Number and place value: P8
At this level, students extend understanding of place value by interpreting, comparing and ordering decimal numbers including tenths, hundredths, thousandths and beyond. Students apply multiplicative thinking to explain and model the relationship between consecutive places (e.g. one-tenth is equivalent to 10-hundredths and 100-thousandths).
Students represent, locate and compare decimals expressed to a different number of places and justify their thinking using mathematical terminology (e.g. 3.5 is larger than 3.458 as 3.5 has five-tenths and 3.458 only has four-tenths).
Students can rename decimals when multiplying and dividing by 10 (6 divided by ten = six-tenths; or 0.3 multiplied by 100 as 30) to assist mental computation. They use their understanding of place value to explain why, for example, the answer to 0.3 x 100 could not be 300.
Ensure that students understand the importance of internal zeros as place holders, and interpret decimals when used in measurement units (e.g. understand the difference between 2.3 metres and 2.03 metres).
Teaching and learning summary:
- Ensure that students can make connections between fractional language and decimal notation (e.g. tenths, hundredths and thousandths).
- Emphasise the extension of the base ten system when working with decimals (one of the larger units is equivalent to ten smaller units and vice versa).
- Note the symmetry of the place value system around the units (e.g. tens to the left of the units and tenths to the right).
Students:
- demonstrate their understanding of the base ten system and generalise this understanding to decimals (tenths, hundredths, and thousandths)
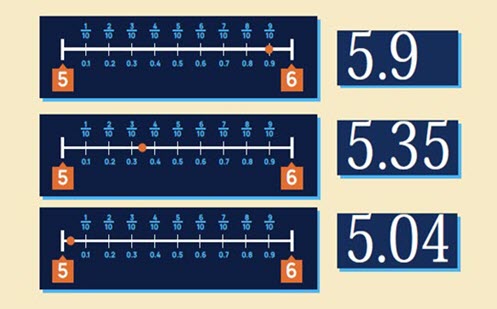
- understand how whole units can be made up of different decimal fractions (10-tenths and 100-hundredths), and place decimals with varying numbers of decimal places on one number line
- use decimals in real-life examples for measurement and money and explain how tenths and hundredths are represented.
Some students may:
- think that the symmetry of the columns is around the decimal point and so they conjure a new column which they often refer to as the ‘oneths’. Help students understand that there is symmetry to the left and right of the ones column, and that ten of a smaller unit makes one of the next (e.g. ten-tenths becomes one whole).
- use incorrect language to describe decimals. Difficulties usually occur because place value is not used when naming numbers and numbers are said as separate digits (e.g. three point four five). The correct place value language should be used to prevent whole number thinking (i.e. 3 and 45-hundredths).
- think ‘longer is larger’ when comparing decimals due to a lack of understanding of how each unit is broken into 10 smaller units (e.g. thinking 4.7 is smaller than 4.19).
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to use place value to compare decimals.
Why are we learning about this?
- Comparing the value of numbers (decimals) helps in daily activities.
What to do
1. Read this table which shows Ali’s long jump attempts.
| Attempt | Distance |
| 1 | 1. 289 metres |
| 2 | 1.237 metres |
| 3 | 1.239 metres |
2. Show each attempt on the same number line below.
3. Use a different colour for each number.
1.2 m 1.21 m 1.22 m 1.23 m 1.24 m 1.25 m 1.26 m 1.27 m 1.28 m 1.29 m
4. Explain which jump was the longest distance and how you used place value to prove your thinking.
Success criteria
I can:
- represent decimals on a number line
- order decimals using place value
- compare decimals using place value and explain my thinking.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -

Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Dividing by 10
This activity supports students to anticipate the result of dividing a whole number by 10. The quotient is extended to include three-digit and four-digit whole numbers.
Go to resource -

Dividing by 100
This activity supports students to anticipate the result of dividing a whole number by 100.
Go to resource -

Place value inquiry
The prompt is a number line with a microscopic view of a section of the line. Students discover the relationship between different parts of the number line and how to divide a larger decimal part into smaller parts.
Go to resource -

Decimal fractions: Video and teaching guide
Use this video to explore decimal fractions, how they are represented and how we use them in day-to-day contexts.
Go to resource

