Expected level of development
Australian Curriculum Mathematics V9: AC9M6SP02
Numeracy Progression: Positioning and locating: P5, Number and place value: P9
At this level, students locate and describe the position of objects using coordinates on the Cartesian plane in all four quadrants.
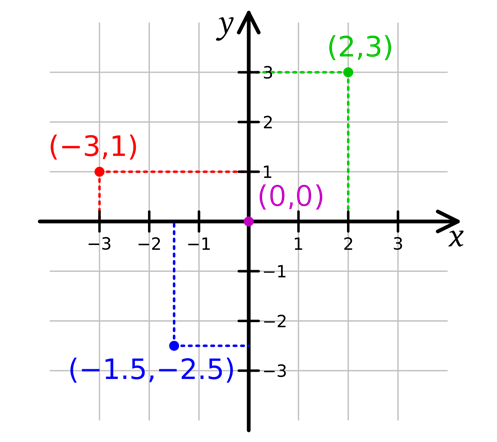
The coordinates, referenced as an ordered pair x and y, for example, (3, 4) locate a position on the Cartesian plane.
Introduce the Cartesian plane in the first quadrant and make explicit that the Cartesian plane is defined by two perpendicular number lines: the x-axis, which is horizontal, and the y-axis, which is vertical. Model how to locate any point in the plane using an ordered pair of numbers. Make explicit the importance of the correct order within the coordinate pairs – x is always first, followed by y.
Revise negative numbers before plotting coordinates in the other three quadrants. This will help students locate the position of coordinates that contain negative numbers.
Use engaging tasks and problems for students to solve that provide a meaningful use of plotting points, for example, to create a shape or work out a shape from a set of ordered pairs.
When teaching and learning about the Cartesian plane, there is an opportunity to connect to to the Number strand and investigating everyday situations that use integers: locate and represent these numbers on a number line (AC9M6N01).
Teaching and learning summary:
- Model the plotting of coordinates on the Cartesian plane.
- Use engaging tasks and problems for students to solve that provides a meaningful use of plotting points on the Cartesian plane.
- Incorporate transformation of 2D shapes using the Cartesian plane.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to locate and describe the position of objects using coordinates on the Cartesian plane in all four quadrants.
Why are we learning about this?
- The Cartesian plane allows us to visually plot pairs of points (x,y).
What to do
- Here are the coordinates of some quadrilaterals, but in each case one coordinate is missing! The coordinates are given going round each quadrilateral in an anti-clockwise direction.
- (2,7), (7,7), (7,5), (?,?)
- (2, 5), (4,5), (4,-2), (?,?)
- (4,3), (6,3), (6,1), (?,?)
- Find the missing coordinates and plot them on the Cartesian plane.
- The three quadrilaterals join together to reveal a mystery letter of the alphabet.
What is the mystery letter?
- The three quadrilaterals join together to reveal a mystery letter of the alphabet.
- Open the interactive tool, Shape Drawing on Grid.
- Plot a series of ordered pairs to form a letter of the alphabet. Note: you need to enter ordered pairs in brackets, (4,5).
- Take a screen capture or plot the points on a grid.
Success criteria
I can:
- plot points on the Cartesian plane
- understand how to read the coordinates of points plotted on the Cartesian plane
- plot and label points, given the coordinates, on the Cartesian plane.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Differentiated teaching
Differentiation involves teachers creating lessons that are accessible and challenging for all students.
Go to resource -
Worked examples
A worked example is not just a pre-worked question that is given to the students.
Go to resource -
Mathematics investigation
At its core, mathematics is about problem-solving and modelling the world around us.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Osprey ranking threats
In this lesson, students work in groups to rank a list of key threats and collate the data in a class spreadsheet.
Go to resource -
Points on the coordinate plane
Explore and extend the coordinate plane.
Go to resource -
Constructing the coordinate plane
Investigate different ways of creating a coordinate plane.
Go to resource -
Shapes on the coordinate plane
Students use the coordinate plane to solve problems and puzzles.
Go to resource -
The fly on the ceiling
Students use an interactive in the form of a game to work out the points on the coordinate plane and enter the paired coordinates.
Go to resource -
Coordinate planes and architecture
Students use the distance between points on a coordinate plane to calculate the perimeter of a polygon.
Go to resource -
Introducing the Cartesian coordinate system
This resource for both teachers and students explores the Cartesian coordinate system. The student section includes self-check questions.
Go to resource -
reSolve: Location – My place in space
Students learn to plot points on the Cartesian plane and find the coordinates of given points. They measure distances between points.
Go to resource
