Planning tool

Students:

• perform and describe positions and orientation of shapes under combinations of transformations
• describe transformations on a cartesian plane
• create tessellations using a combination of transformations.

Some students may:

• believe that when 2D shapes are transformed, their initial properties change. To address this, expose students to a range of experiences to aid conceptual development of transformation. Gauge whether students can generalise that when 2D shapes are transformed they still retain their initial properties.
• have difficulty reflecting an object when the mirror line is at an angle (other than horizontal or vertical). Support students with a visual aid such as a plane mirror to show where the reflected object is mapped.
• use the incorrect fixed point when rotating a shape. Support students by providing them with the original diagram on a sheet of paper as well as a transparent sheet with the same display. The transparent sheet covers the original paper and a pin is placed through both sheets on the point of rotation. The original sheet remains in the original position, while the transparent sheet is rotated displaying the various positions of rotation.
• have difficulty when plotting a shape on Cartesian plane if unfamiliar with negative numbers, particularly in quadrants other than the first. Link learning about transformation with learning about the Cartesian plane.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are learning how to model and describe the effects of transformations by flipping, sliding and turning 2D shapes.
• We are developing our understanding and skills in transformations including reflections (flips), translations (slides)
  and rotations (turns).

Why are we learning about this?

• Transformation is a way of organising space. Tessellations can be found in quilts, tiling and architecture.

What to do

Today I am going to show you how to make a simple tessellation pattern.

1. Create this rectangular shape called a ‘tromino’ on a sheet of paper or copy into a new document.

   

   If you are making the shape on a sheet of paper you will need to cut out 16 to make the tessellation.

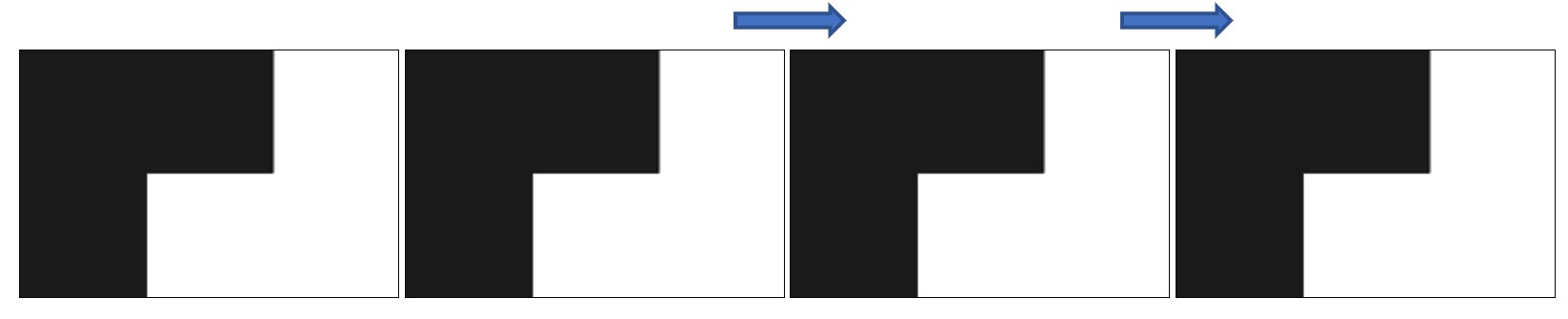
2. Start the pattern with the first shape, then slide the shape along.

   

1. Do two more slides of the shape

   

2. Now rotate the shape one half turn (180˚) and slide down

   

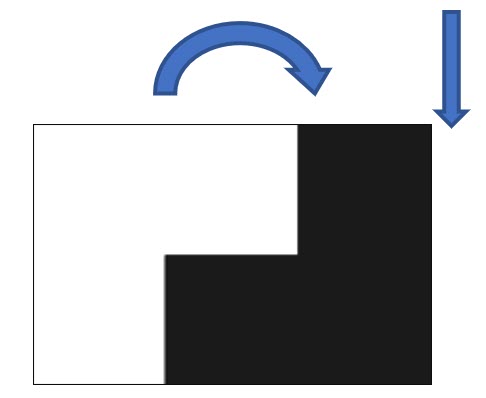
3. Slide this shape along 3 times. Yours won’t have gaps. This is just to make it easier to see the transformations.

   

3. The tessellation will look like this:

   

Success criteria

I can:

• perform and describe positions and orientation of shapes
• create tessellations using a combination of transformations.