Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7A02, AC9M7A06
Numeracy Progression: Number patterns and algebraic thinking: P6, P8
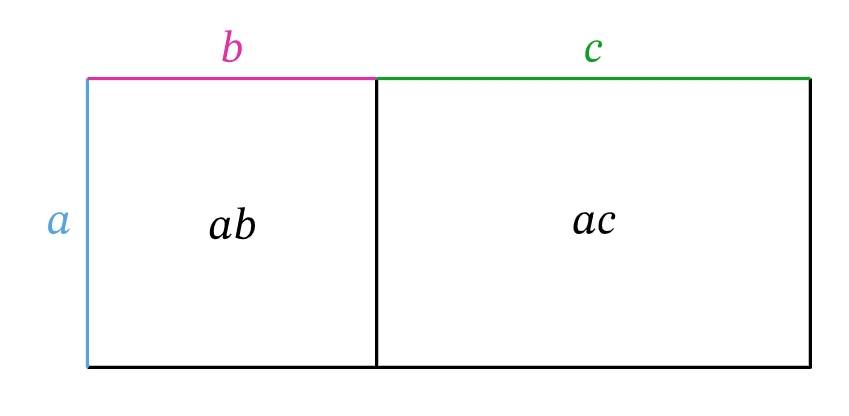
At this level, students understand and apply arithmetic knowledge to formulate algebraic expressions and equations. By spending time on worded problems that present relationships between variables (for example, Volume = length × width × height), it will help students to identify and assign pronumerals (V, l, w, h).
Give multiple opportunities for students to formulate equations. Use digital tools to do this or analyse various tables with differing values. Consider using the formula function in Excel spreadsheets, for instance.
Question students on what they notice about their equation when values are changed incrementally and when operations are switched – a plus to a minus. This approach helps students to visualise manipulations of algebraic expressions so that they may carefully construct expressions when new variables are introduced.
Highlight to students that using correct algebraic language is important and that the rules we use with numbers also apply to variables. Emphasise that pronumerals stand in for variables or numbers. Be specific when explaining expressions and equations. Say 'three lots of x is added to two lots of x to give a total of five lots of x’ and not 5x2, which should be said as 'five lots of x squared’.
Emphasise that equations must be balanced on each side of the equals sign, and that there are arithmetic laws (for example, associative, distributive) to follow when approaching problems.
Revising the following rules is recommended for this topic:
- the associative and distributive laws
- the array model for multiplication
- the term ‘inverse’
- the order of operations and use of brackets
- the difference between a coefficient and a power/index.
Teaching and learning summary:
- Introduce the concept of pronumerals as representations of numbers/variables.
- Demonstrate how to form an expression, or equation, from a worded problem.
- Bolster learning with tables and Excel spreadsheets using the formula function and digital software programs.
- Use systematic approaches to help students formulate algebraic equations correctly.
Students can:
- write an expression or equation from a worded problem using pronumerals
- manipulate pronumerals in expressions mathematically and recognise the relationship between variables and how they change
- take a systematic approach to make algebra achievable and meaningful
- apply arithmetic rules to expressions involving variables.
Some students may:
- believe that pronumerals stand for a specific amount or unit of measurement.
- confuse the variable 'x' with the multiplication symbol.
- not recognise that an algebraic expression can be an answer to a problem; they feel that there should always be a numerical answer.
- think that 3x + 2x = 5x2 or that 3x × 2x = 6x.
- add together unlike terms. For example, 2x + 3y ≠ 5xy or 2x + 7 ≠ 9x.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to do maths with letters (variables).
- We are learning how to transform everyday scenarios into mathematical expressions.
- We are learning that the rules we already know about numbers also apply to letters (variables).
Why are we learning about this?
Why? Because mathematics is so much more than numbers. Once we can describe our world with mathematical symbols, we can perform all kinds of interesting calculations about it and make predictions about the future.
What to do
- Go to the place in your house where the fruits and vegetables are. Wherever that is, I want you to choose a letter to represent that place. Is it the fridge? Then we will call it ƒ. Is it the pantry? We’ll call that p. Maybe it’s the garden; you can call that g. We’ve now created our first ‘variable’.
- Make a list of three of the fruits or vegetables you find there, for example, 3 apples, 2 cucumbers and 4 tomatoes.
- Now, instead of referring to them by their name, I want you to select a single letter for each instead. We will also use a + symbol to show that each of vegetable or fruit is on our list. The example above can be shortened to: 3a + 2c + 4t.
- Let’s combine this information into a mathematical sentence. I’ll do it first. In my fridge there are 3 lemons, 5 onions and 4 potatoes. So, I will turn this information into the mathematical sentence: ƒ = 3l + 5o + 4p
- You could try repeating this for other parts of your house, for example, my wardrobe has 5 shirts, 3 jeans and 4 T-shirts:
w = 5s + 3j + 4t
Now that we know how to create mathematical sentences, we need to practise the rules of manipulating them.
Consider this word problem
Raj opens his fridge (ƒ) and finds 3 litres of cow’s milk (c) inside. So ƒ = 3c
A little later, Raj’s mum returns from the supermarket with an extra 2-litre bottle of cow’s milk, along with 2 litres of soy milk (s) and 1 litre of oat milk (o).
Can you update the mathematical sentence above to include the new items?
If you're not sure, this is how I did it.
I did this in two steps.
- ƒ = 3c + 2c + 2s + 1o
- ƒ = 5c + 2s + o
Two important rules are illustrated in the example above.
- Firstly, we can only add things together if they have the same letter. We can’t describe Raj’s fridge as ƒ = 8cso because then we wouldn’t know how many litres of each type of milk Raj has.
- Secondly, we can shorten our sentences even more, by removing the number 1 from the front of variables. Whenever you see a variable on its own, there is an invisible 1 hiding in front of it.
Your final task
Before someone at your house goes to the shops, I want you to create a new mathematical sentence about some of the items in your fridge. Then, when they return, I want you to update that sentence to show which items have been increased and which new items have been added.
Success criteria
- I can describe the items I find in different parts of my house using variables and mathematical sentences.
- I can update my mathematical sentences with new information and follow the correct rules about adding variables.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Expressions, formulas and substitution
In this lesson, students will explore substituting values into familiar and unfamiliar formulas to determine an unknown.
Go to resource -
Formulating algebraic expressions
This lesson encompasses students’ introduction to formal algebraic concepts.
Go to resource -

Introduction to algebra
From the AMSI Supporting Australian Mathematics Project, this resource gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions. This resource focuses on introducing algebra and the use of pronumerals.
Go to resource -

reSolve: Prisms and pyramids
This resource encourages students to make connections between their knowledge of 3D shapes and algebra. They look for the connection between the number of faces, edges and vertices and find a general rule (Euler's formula). The resource includes teacher notes and student sheets.
Go to resource -

The laws of arithmetic and their use in algebra
From the AMSI Supporting Australian Mathematics Project, this resource gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions. This resource focuses on how to manipulate pronumerals in algebraic expressions.
Go to resource -

More number pyramids
This resource allows for a systematic approach to solving a number problem. The interactive game demonstrates visually to students how changing one variable influences the others. Patterns emerge and algebraic expressions could be built.
Go to resource -

Rewriting expressions using the distributive property
This site gives teachers a step-by-step approach for guiding students on using the distributive property. It includes lesson plans, an explainer and a worksheet.
Go to resource
Assessment
By the end of Year 7, students can formulate algebraic expressions that represent mathematical relationships between variables. Students use constants, operations and brackets in their expressions.
-

Planning a pizza party
In this lesson, students work collaboratively to identify variables and constraints to build algebraic expressions. This resource includes lesson activities with questioning and explanation as well as practice questions.
Go to resource -

Special numbers
This resource presents a puzzle that gives students the opportunity to approach the problem in different ways. This could be a collaborative task where using algebraic thinking will help to solve this puzzle.
Go to resource