Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7N08
Numeracy Progression: Multiplicative strategies: P9, Interpreting fractions: P8, Proportional thinking: P3
At this level, ratios are introduced as a method of comparing quantities. Students learn how to recognise and represent these comparisons to solve problems. The concept of dividing a quantity by a given ratio is also introduced.
Showing students multiple examples of practical situations where students may meet ratios will support them in developing their understanding. Use visual or digital aids to show the quantitative relationship between two or more groups, for example, following a cake recipe.
There are many connections between ratios and fractions, such as simplifying and equivalence, but students should be aware that ratios can have more than two parts. Ensure students are competent with using fractions and use part-part and part-whole models to visualise ratios, for example, a cherry diagram or bar model.
Make connections to real-world examples to bolster understanding referring to sharing and dividing quantities (for instance, money or lollies) between two or more people. Use questioning to uncover recognition of part in a worded problem and relate it with diagrams and represent ratio notation. Solve problems further with the addition or subtraction of fractions.
This topic has many connections with other areas in the mathematics curriculum, for example, fractions, percentages, graphs and algebra.
Teaching and learning summary:
- Introduce the concept of ratio as a comparison of quantities. Use part-part and part-whole explanations as a visual aid.
- Discuss how a ratio is displayed – whole numbers, same units.
- Show how to ‘share’ and divide a given quantity by a ratio.
- Use diagrams and virtual material to represent ratios.
- Enable recognition, representation of parts and wholes to solve numerical and real-life problems.
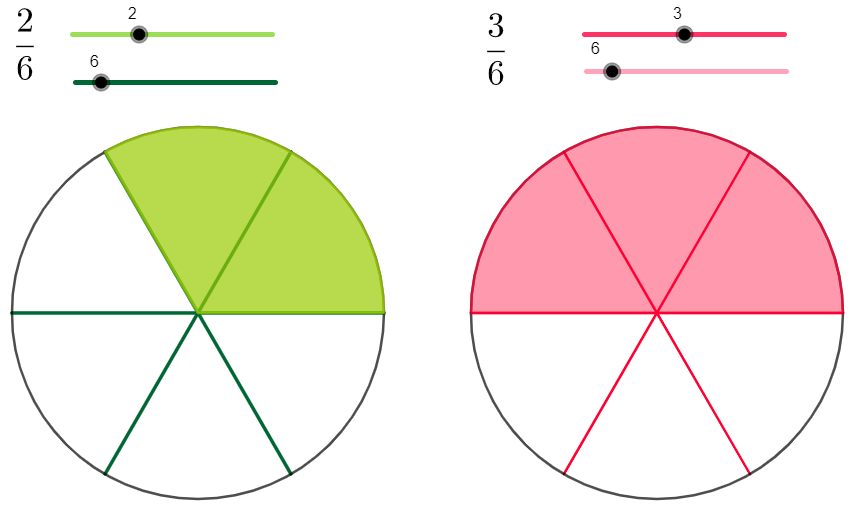
Students:
- understand that a ratio is a comparison of quantities
- convert from one unit of measurement to another
- correctly express the comparison of two or more amounts as a ratio
- express a ratio using whole numbers
- can simplify a ratio
- recognise ratios using diagrams, physical material or virtual material
- represent ratios numerically and use fractions to solve problems
- recognise and represent ratios in real-world scenarios to solve problems.
Some students may:
- not understand that proportional reasoning is about comparing two quantities and fail to identify the variables that are to be compared.
- confuse parts of a ratio as fractions, that is, they see 3:4 as three parts of a whole rather than a whole divided into seven parts, made up of 3 parts ‘and’ four parts.
- struggle with which part of a ratio comes first, especially with unit ratios and best buys.
The following resources address common misconceptions with ratios and proportion, and give strategies to address them.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to compare ratios.
- I am learning the meaning of the term 'ratio'.
- I will apply various strategies to solve ratio problems.
- I will simplify ratios.
Why are we learning about this?
Ratios are frequently used in our daily life to simplify problems and describe different aspects of a given situation. This activity explores fractions, ratios and proportionality.
What to do
You and a friend are sharing 45 lollies between the two of you. This is not an even number so you decide to explore how the lollies could be shared. You begin with five lollies for your friend, four for yourself, five for your friend, four for yourself, and so on.
1. How many lollies will you have once you have divided them all?
2. How many lollies will your friend have?
3. Rather than handle the lollies every time, you decide to get mathematical and draw up a table to see what happens for the different ratios:
- 5:4
- 2:3
- 7:2
- 1:2
4. Complete the table below.
| You : Me | Friend's total | My total | Total shared |
| 5:4 | |||
| 2:3 | |||
| 7:2 | |||
| 1:2 |
5. What patterns do you notice in your table?
Challenge
How would you share 45 lollies if there were three people to the ratio:
-
2:3:4
-
4:2:3
-
1:2:2
Success criteria
- I can compare ratios.
- I can use a diagram to represent ratios.
- I can understand what ratio means.
- I can simplify ratios.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Proportional reasoning: Video and teaching guide
Use this video as a springboard to explore scaling or proportional thinking, and to apply that thinking to a food-related context, drawing on reasoning and mathematical modelling.
Go to resource -

Practical numbers: Part 1
In this lesson, students explore standardised measuring systems.
Go to resource -

Practical numbers: Part 2
In this lesson we use the context of an ancient bazaar to investigate measurement systems.
Go to resource -

Patterns, rules and graphs
In this lesson, students use games to learn about space and location on a Cartesian plane.
Go to resource -

Recognise and solve problems involving simple ratios
This is a teacher-facing resource that provides guidance, worked examples and activities about comparing quantities using ratios as well as making meaning between different formats of the same ratio.
Go to resource -

Proportional relationships and percentages
This series of lesson plans, materials and assessments gives detailed step-by-step advice on proportion and scaling. The various resources for this topic allows for differentiation in the classroom.
Go to resource -

Ratio or proportion?
This article is perfect for teachers, giving lengthy guidance on teaching the concepts of ratio and proportion and the difference between them.
Go to resource -

First steps into proportions: comparing ratios
Students use this practical interactive to visually connect fractions, ratios and proportion.
Go to resource
Assessment
By the end of Year 7, students can recognise, represent and solve problems involving ratios. Students understand that ratios express the quantitative relationship between 2 or more groups.
-

Using proportional reasoning
This lesson assesses students’ ability to use proportional reasoning. Students demonstrate their ability to describe a ratio, to express a ratio in different ways, and to answer contextual problems.
Go to resource -

Mixing lemonade
In this interactive activity, students use the concepts of ratio and proportion to mix lemonade to a given strength. Teacher notes and extension suggestions are also included.
Go to resource -

Defining equivalent ratios
This interactive activity assesses students' ability to understand visual representations and numerical representations of ratio, proportions and fractions.
Go to resource