Expected level of development
Australian Curriculum Mathematics V9: AC9M9N01
Numeracy Progression: Interpreting fractions: P9, Number and place value: P10
At this level, students work with the real number system and recognise both rational and irrational numbers when working on a variety of mathematical problems. Students are fluent in integer arithmetic, fractions and decimals, and now further their skills, applying them to a range of contexts.
Students should expect that solutions to practice problems will often not be round numbers. Fractions and decimals become fully integrated into mathematics and students should be encouraged to see them as different to natural numbers. Start by asking 'How many rational numbers exist between 0 and 1?'
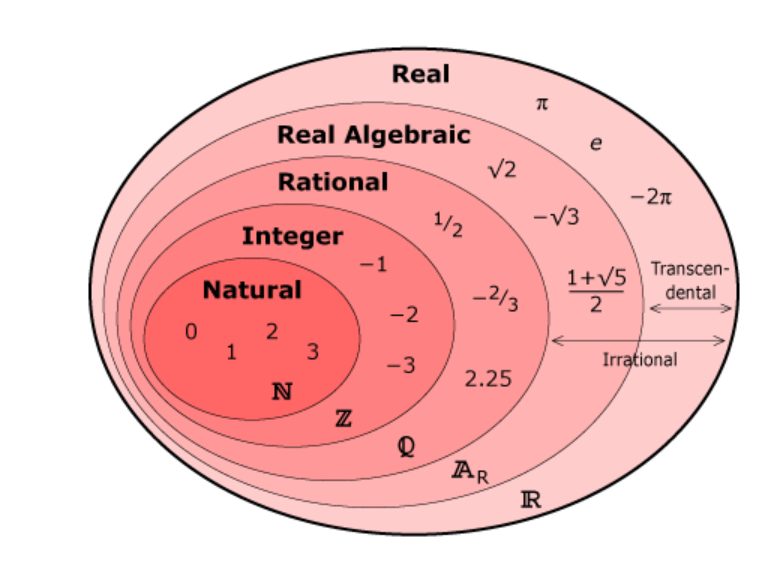
Show students how to diagrammatise number sets in concentric circles, starting with natural numbers in the middle and working outward. Students can define different number sets and the rationality of a number on their diagrams, providing examples.
Take the opportunity to conduct classroom talks to increase engagement and to connect why students need to define, know and use irrational numbers. You may wish to give context discussing the history of numbers starting with the ancient Greek mathematicians who believed irrational numbers existed (to their detriment); the paradox of a number that has infinite decimals; and how a number that can go on forever can still be drawn and its lengths measured (1, 1, √2).
The position of rational and irrational numbers can be demonstrated using number lines where a sequence of irrational numbers fits between rational numbers.
Students are required to substitute real numbers into various formulas. Provide extensive practice evaluating formulas when a fraction is substituted as the variable. This skill base naturally points towards algebra, but it is important to scaffold why you would be working with variables representing numbers. For example, students might find the circumference of a circle and be given the variables in the context of a worded problem. Students recognise that answers involving π (pi) can be corrected to a certain number of decimal places or can be represented in symbolic form. Encourage students to see writing an exact answer as a form of shortcut. Explain that π has infinite decimals, so instead of writing an answer that is never ending, or rounding π and losing accuracy, it is often shortened and represented in symbolic form.
Use digital formats to help with calculations and digital software to simulate various problems to allow for visual representations and repeated practice.
Teaching and learning summary:
- Develop confidence in performing routine mathematical skills with fractions.
- Define the concept of an irrational number as one that is unable to be expressed as a fraction.
- Zoom in on a number line to explore the infinite space between the natural numbers.
- Explore the history of irrational numbers and the Pythagoreans.
- Discuss the difference between exact and approximate values, and the scenarios in which each might be used.
- Practise presenting solutions in exact form, including roots and π.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
The real numbers
This AMSI guide covers years 8 to 10, given the extent of this topic on working with real numbers. Allowing for differentiation, find the relevant sections, worked examples, questions, explanations and required knowledge.
Go to resource -
Keeping it real
This activity is an exploratory activity on real numbers and gives explanations for students to follow, including a downloadable series of identification questions with answers.
Go to resource -
Ordering real numbers
Students are asked to order real numbers from least to greatest. Students reset the activity to practise many times.
Go to resource -
Representing situations with inequalities
This lesson plan, teacher guide, presentation slides and student material work with the various ways inequalities are modelled and represented in maths.
Go to resource
Assessment
By the end of Year 9, students can recognise and use rational and irrational numbers to solve problems.
-
Keeping it real
This activity on real numbers includes a downloadable series of identification questions with answers suitable for a formative assessment in class or homework.
Go to resource -
Two cubic equations
This task is a mathematical investigation into a problem using various types of numbers that are represented in one algorithm. Students are required to find the values of the variables and limits provided.
Go to resource