Expected level of development
Australian Curriculum Mathematics V9: AC9M9P02
Numeracy Progression: Understanding chance: P6
At this level, students build on their knowledge of probability, Venn diagrams, two-way tables and the terms ‘and’ and ‘or’ (inclusive or exclusive) in relation to events whereby relative frequencies may be calculated.
By showing students similar 'and' and 'or' set-ups and then representing these outcomes on Venn diagrams, students can visualise the similarities and differences between the conditions. It also highlights the importance of correctly designing an experiment from a large data set.
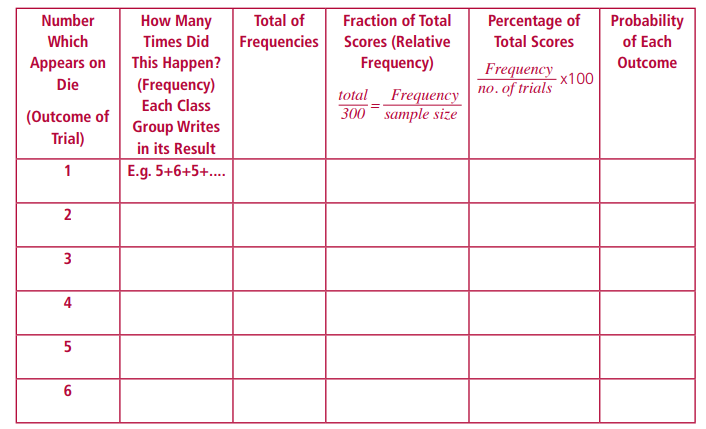
Provide data or materials for students to use their own experimental data to calculate relative frequencies and make probability estimates. Make explicit how to calculate relative frequencies using the number of times a particular event occurs and dividing it by the total number of trials for a given experiment.
Discuss and model the use of Venn diagrams and two-way tables to represent inclusive and exclusive events. Use worked examples when making probability calculations for events, applying the terms 'and' for inclusive events and 'or' for exclusive events.
Make connections to the practical use of large data sets to show that we can make predictions for a variety of reasons, such as decision-making in health and medicine, weather conditions and insurance.
Teaching and learning summary:
- Review students’ knowledge and understanding of probability.
- Introduce the meaning of the terms ‘and’ and ‘or ’ in a probability context.
- Introduce the concept of relative frequency and estimated probability.
- Revise and extend how to use Venn diagrams and two-way tables to represent relative frequencies of events.
- Enable students to use their own experimental data.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Egg roulette: Part 1
In this lesson students use a fun context to learn about probability without replacement.
Go to resource -
Egg roulette: Part 2
In this lesson, students explore simulations to address misconceptions related to probability with and without replacement.
Go to resource -
Using tables for conditional probability
This resource provides teacher guidance, lesson plans and practice around creating tables to house outcomes of conditional probability.
Go to resource -
Chance
In this resource, teachers are shown how by changing their questions they can guide students to successfully solve problems and understand new concepts. Specific examples on this topic can be found on p. 18.
Go to resource -
Two-way tables
In this lesson, students learn to construct and use two-way tables using everyday language and data sets. There are teacher notes, presentation materials, student worksheets and assessment questions.
Go to resource -
Relative frequency tables
In this lesson students learn to construct and use relative frequency tables. There are teacher notes, presentation materials, student worksheets and assessment questions.
Go to resource -
Probability and relative frequency
These detailed lesson plans provide content knowledge, context and activities to enable teachers to explain relative frequency using a meaningful context. The resource includes student worksheets.
Go to resource
Assessment
By the end of Year 9, students can calculate relative frequencies from given or collected data and assign probabilities to the outcomes of these compound events.
-
Using tables for conditional probability
An excellent resource for students to practise creating tables to systematically record outcomes of conditional probability.
Go to resource -
Two-way tables
In this lesson, students learn to construct and use two-way tables using everyday language and data sets. There are teacher notes, presentation materials, student worksheets and assessment questions.
Go to resource -
Relative frequency tables
In this lesson students learn to construct and use relative frequency tables. There are teacher notes, presentation materials, student worksheets and assessment questions.
Go to resource