Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9ST03
Numeracy Progression: Interpreting and representing data: P8
At this level, students have knowledge of various representations of data and can now extend this to comparison. Students compare many data sets of numerical variables to make comparisons using appropriate mathematical vocabulary. Students consider the shape and spread of the distributions of data, consider the distribution of the centre, and make note of outliers making comment on symmetry or skew.
When data representations are compared, students must choose the same form of representation, for example, stem-and-leaf plots. Leaf plots are easy to compare. Demonstrate to students that comparisons between plots should be ordered from smallest to largest from the left of the stem. Histograms are also easy to compare because they are set up with identical class intervals. Show students a variety of pairs of graphs and ask students to consider which are suitable for comparison and why.
Histograms plot data about frequency and, like stem-and-leaf plots, are easy to compare with each other.
Ensure students know how to find, calculate and represent different plots for numerical data. Explicitly teach the main features of distributions using the language of statistics appropriate to this level, such as positive and negative skewness, symmetry, bi-modal and outliers. Students should now be able to select the most appropriate measures of central tendency based on the shape of the distribution.
Work through different examples when describing features visually so that students build visual knowledge of types of distributions, their features and how to make comparisons so that they can analyse data sets and displays. Encourage students to report back using the terminology of statistics, connecting language with what they have learnt.
Teaching and learning summary:
- Revise different types of data displays and ensure students are familiar with histograms, stem-and-leaf plots and dot plots.
- Teach students about the features of displays and how to recognise important concepts like shape and spread, outliers and skewness.
- Discuss what consistencies would be required to use the same type of display to compare two or more comparisons.
- Show students how to describe and compare like sets of data using statistical terminology.
Students:
- can represent frequency data in many different displays
- can work with multiple datasets of the same type side by side
- make comparisons between dataset displays, such as back-to-back stem-and-leaf plots
- analyse, evaluate and interpret results when making comparisons of data displays
- use the language of statistics to describe spread, distribution, outliers, frequency, bi-modal and symmetry.
Some students may:
- not make distinctions between bar charts, which are used for categorical data, and histograms, which are used for numerical data.
- not realise that when comparing back-to-back histograms, the leaves of histograms are ordered smallest to largest from the left of the stem.
- compare distributions using displays with different scales or class intervals.
- confuse negative and positive skews, as these are confusing without a useful memory technique.
- automatically revert to bar graphs rather than choose from a diverse range of displays.
- find it difficult to select appropriate class intervals on histograms.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to represent the distribution of runs in each innings of a cricket test match on comparable displays.
- We will compare these distributions to gain deeper insights into the result of the match.
Why are we learning about this?
It is often said that the Australian test cricket captain is our second-most important leader, behind the prime minister. Unlike the football codes, which vary in popularity from state to state, cricket is a sport that unites us all. And, more than in any other sport, cricket fans are obsessed with stats.
Cricket datasets are as old as the game itself, with pages bursting out of home libraries the world over. Looking back over old scorecards tells a story about the game, but coaches and analysts need to dig deeper to find out how history can help their sides improve. Let’s get a feel for their work using cricket stats.
What to do
- Select any past cricket test match and find the scorecard online. (If cricket isn’t your cup of tea, I’d recommend basketball, netball, soccer or any sport where there are multiple team players per match. Choose a famous match to make it easier to find the scorecard.)
- Going back to the cricket example, use different columns on a spreadsheet, list the runs of each batter in ascending order for each innings.
- Create a histogram to display each innings. Make sure you use the same class interval (bin size) for each batter. Label the graphs clearly and display them side by side.
- Comment on the shape of each distribution. What does the distribution tell you about the performance of the team during the innings? Was it a team effort or did one batsman carry the team? Are there any outliers present?
- Based on the shape of the distribution, determine whether it would be more useful to calculate the median or mean for each innings. Carry out these calculations.
- Compare the measures of centre of the displays to the result of the match. Does your analysis suggest the actual result?
- Imagine you are the team analyst. Write a short set of notes for the coach of the losing team suggesting improvements for a better performance next match.
Success criteria
- I can present multiple datasets on comparable displays.
- I can compare these datasets to gain useful insights.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

How risky is life?
Students interpret data and diagrams, and make interpretations and evaluations. These tasks can be used in class or for assessment purposes.
Go to resource -

Data representation and interpretation
Teachers are given advice on teaching back-to-back stem-and-leaf plots and histograms, and how to use terms such as 'skew', 'bi-modal' and 'spread' to describe, interpret and compare data.
Go to resource -

Data investigation and interpretation
This teacher-facing resource provides guidance on a number of aspects of data displays including histograms and stem-and-leaf plots. It also provides guidance on the shape of displays and how to make comparisons.
Go to resource
Assessment
By the end of Year 9, students can analyse reports of surveys on how data was collected to estimate population means and medians.
-

Comparing histogram, dot and stem-and-leaf diagrams
This interactive allows students to make repetitive evaluations for histograms, stem-and-leaf plots and dot plots. Variations in intervals can also be changed. This activity comes with questions and answers relating to comparison of data.
Go to resource -

Using histograms to answer statistical questions
These two interactive activities relate to interpreting frequency data. Students are stepped through from easy to more difficult questions.
Go to resource -

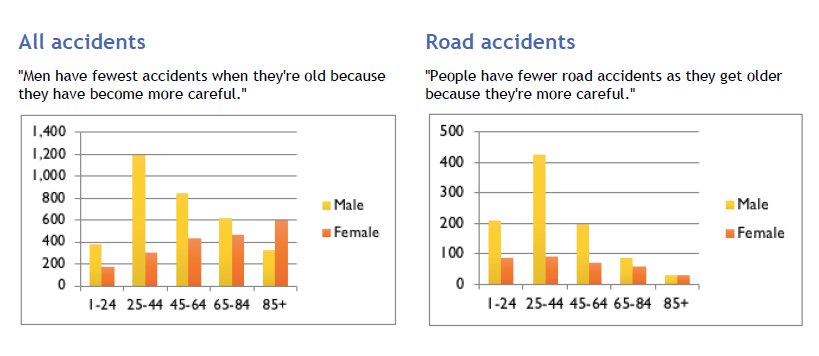
Are males better drivers?
Students work collaboratively to compare data of male and female drivers by drawing the appropriate graphs. The resource includes an assessment rubric and worksheet.
Go to resource