Challenges
Puzzles, brain teasers and maths riddles are a fun way to use your problem-solving skills and logical thinking.
Sharpen those maths skills and have a go at this fun challenge.
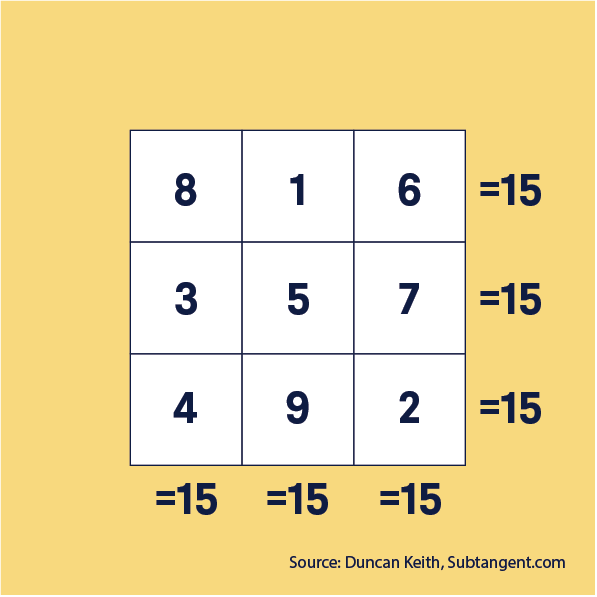
Magic square
Can you put the digits 1 to 9 in a square so that each row, column and diagonal adds up to 15?

Answer
Here is one solution.
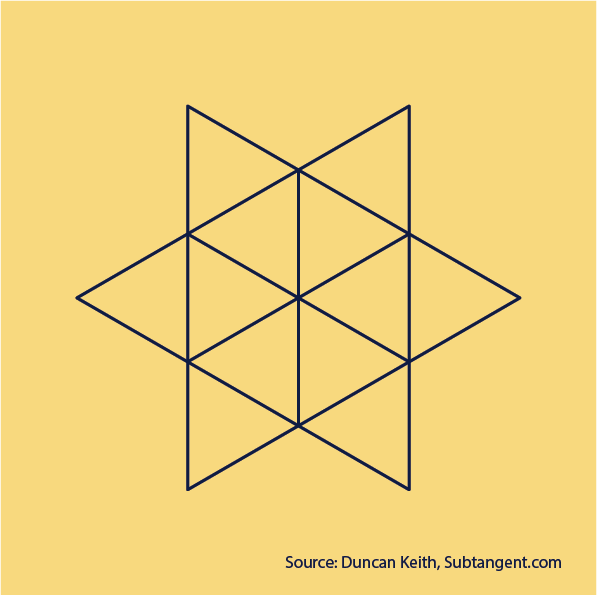
How many triangles?
How many triangles can you find in this pattern?
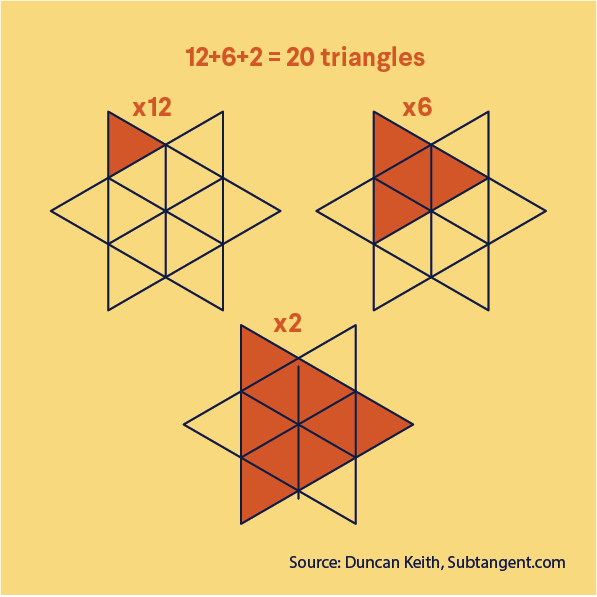
Answer
There are 20 triangles in total. Did you find them all?
Missing number
Can you find the missing number? Which number should go in the empty triangle?
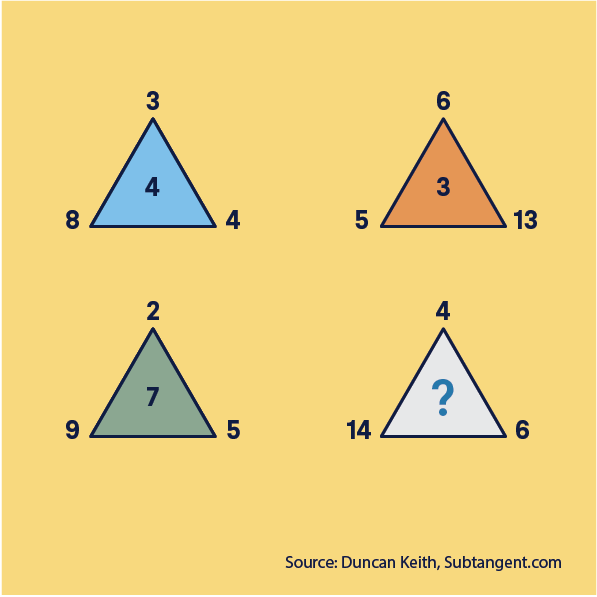
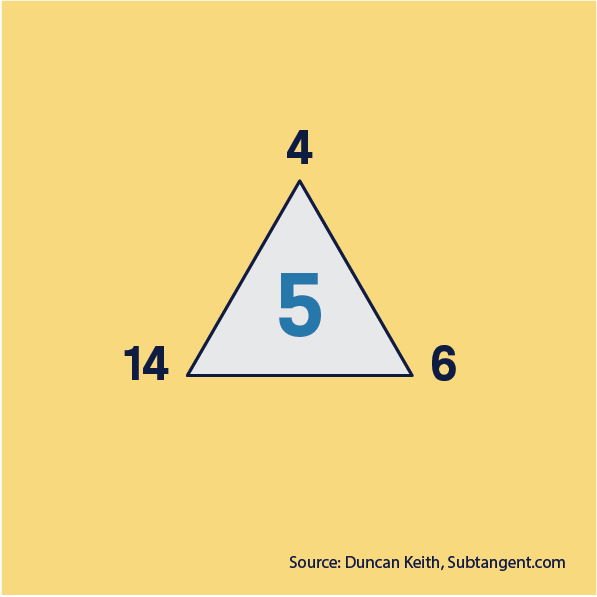
Answer
Did you find the pattern? Add the bottom two numbers and divide it by the top number to find the number in the middle. Therefore, the pattern to find the missing number is: (14 + 6) ÷ 4, which means the missing number is 5.
Fruitful
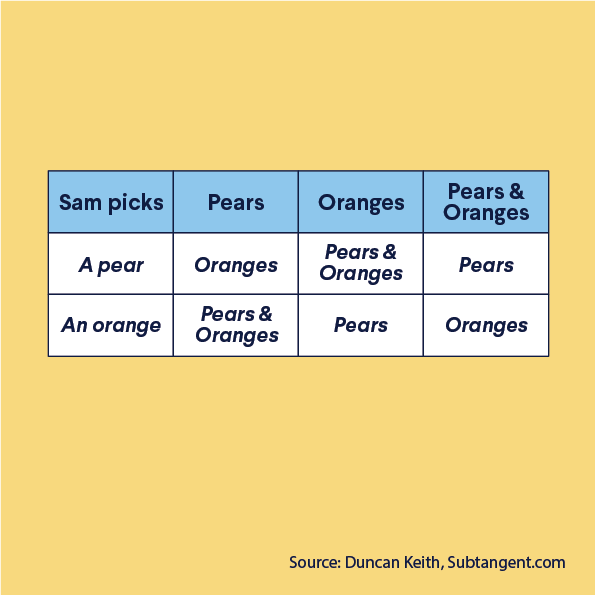
Sam has three boxes of fruit. One contains pears, one contains oranges, and one contains both oranges and pears.
The labels have fallen off and all have been stuck back on the wrong boxes.
Sam opens one box and, without looking in the box, takes out one piece of fruit. Sam looks at the fruit, the label on the box and immediately put all the labels on the correct boxes.
What label was on the box Sam opened and what fruit did they take out?

Answer
There are two possible solutions, here is one:
Sam opened the box labelled ‘Pears & Oranges’. As all labels are wrong, this box must contain only pears or only oranges. If they pick a pear, then they know that the box they opened should be labelled ‘Pears’ and other two should be ‘Oranges’ and ‘Pears & Oranges’. The box labelled ‘Oranges’ should be labelled as ‘Pears & Oranges’ and the box labelled ‘Pears’ should be labelled ‘Oranges’.
Confused? Take a look at this table.
Four lines
Draw 9 dots in a square like this:

Can you draw a line through all 9 dots with just four straight lines?
You can start wherever you like but you can’t take your pen off the paper.
Answer
For this one, you must (literally) think outside the box!
Here is one solution:

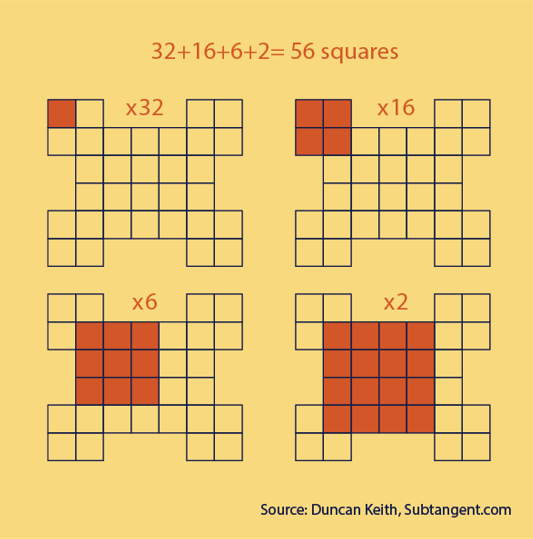
How many squares?
How many squares can you see in this pattern?
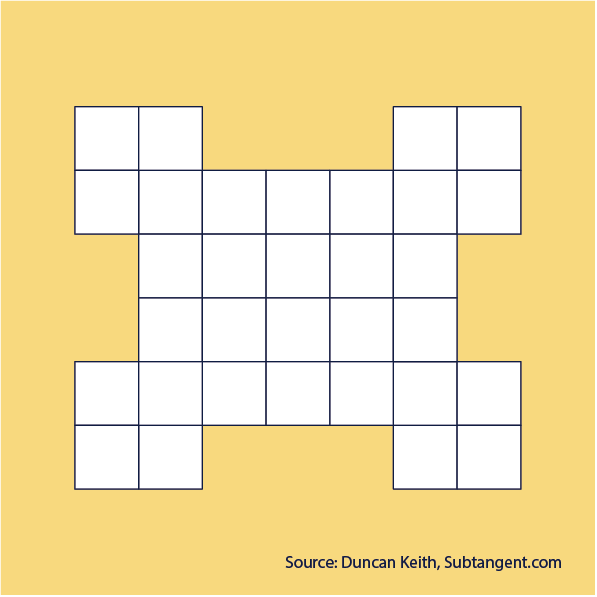
Answer
There are 56 squares in total: 32 at 1 x 1, 16 at 2 x 2, 6 at 3 x 3, 2 at 4 x 4.
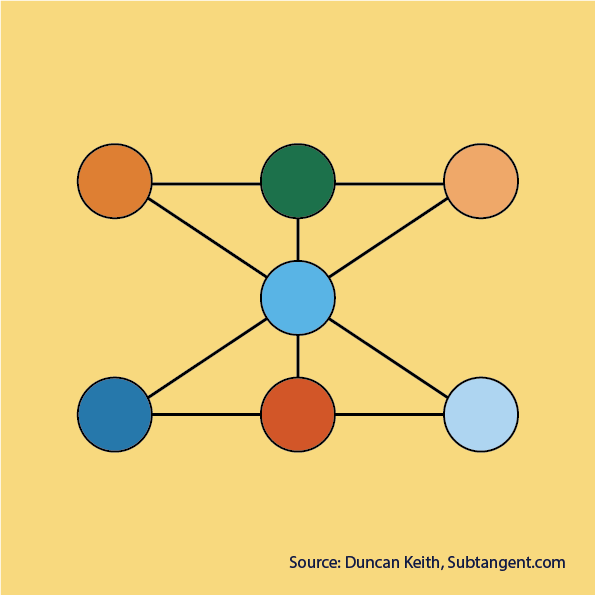
Number lines
Can you put the numbers 1 to 7 in each circle so that the total number of every line is 12?
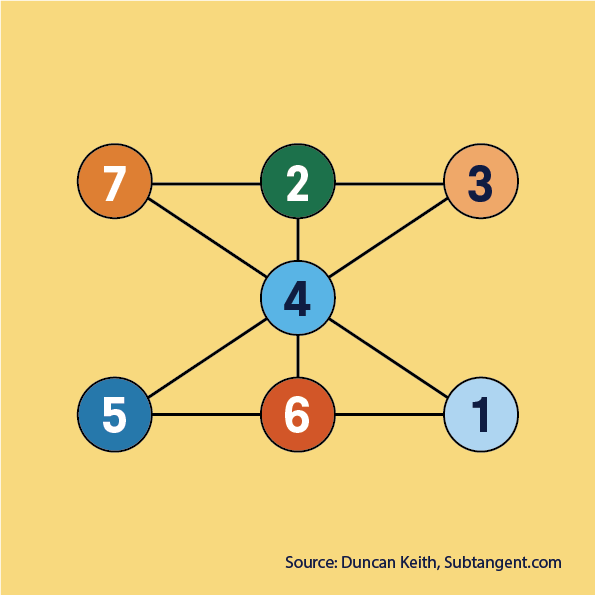
Answer
How did you go? Here is one solution. Teachers, if students get stuck on this one, give them the middle number 4 as a hint.
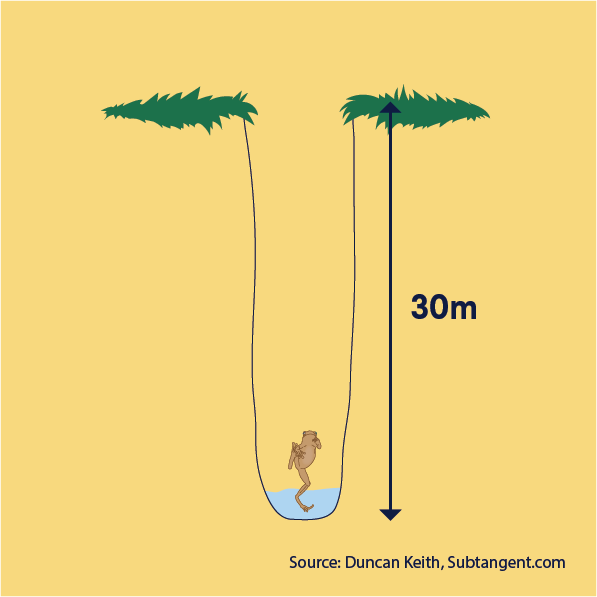
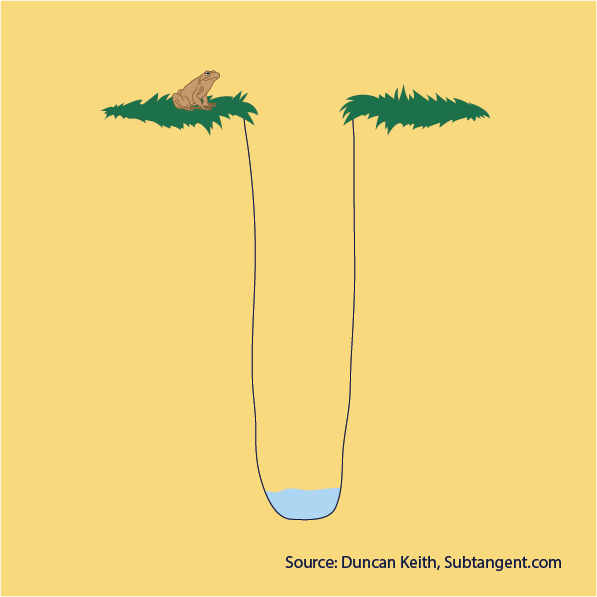
The escaping frog
A frog has fallen into a pit that is 30 metres deep. Each day the frog climbs up 3 metres but falls back 2 metres at night.
How many days does it take for the frog to escape?
Answer
It will take 28 days for the frog to escape. After 27 days and nights the frog only has 3 metres to go. On the 28th day the frog is able to jump to freedom!
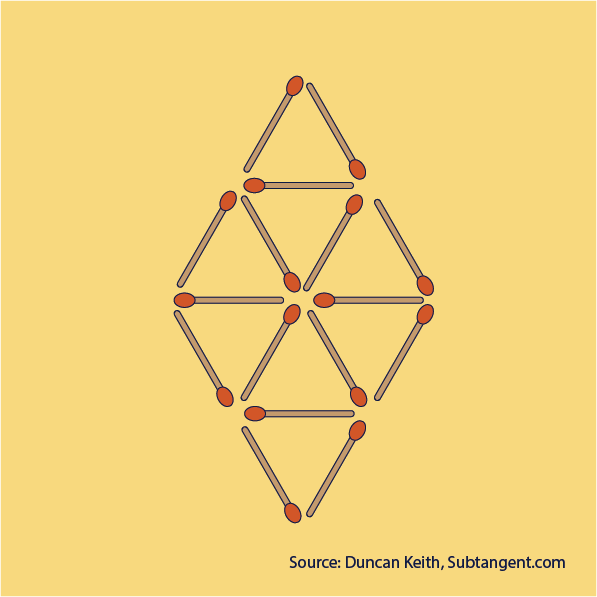
Missing matches
Remove just 4 matches to leave 4 equilateral triangles. Equilateral means all the triangles must be exactly the same size.
Try using real matches or toothpicks to help work through the problem.
Answer
Here is one solution. How many different solutions can you find?

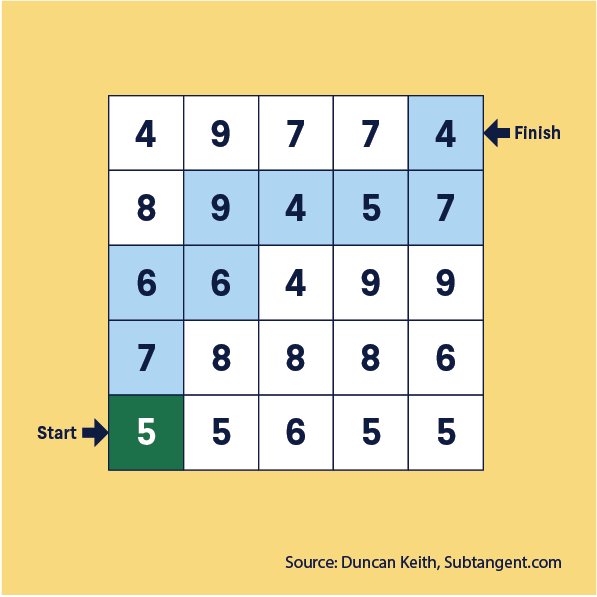
Find the path
Can you find a path adding the numbers as you go to make exactly 53?
Start at the bottom left square (5) and move up, down, left or right until you reach the finish square (4).

Answer
How did you go? Here is one solution:
5 + 7 + 6 + 6 + 9 + 4 + 5 + 7 + 4 = 53
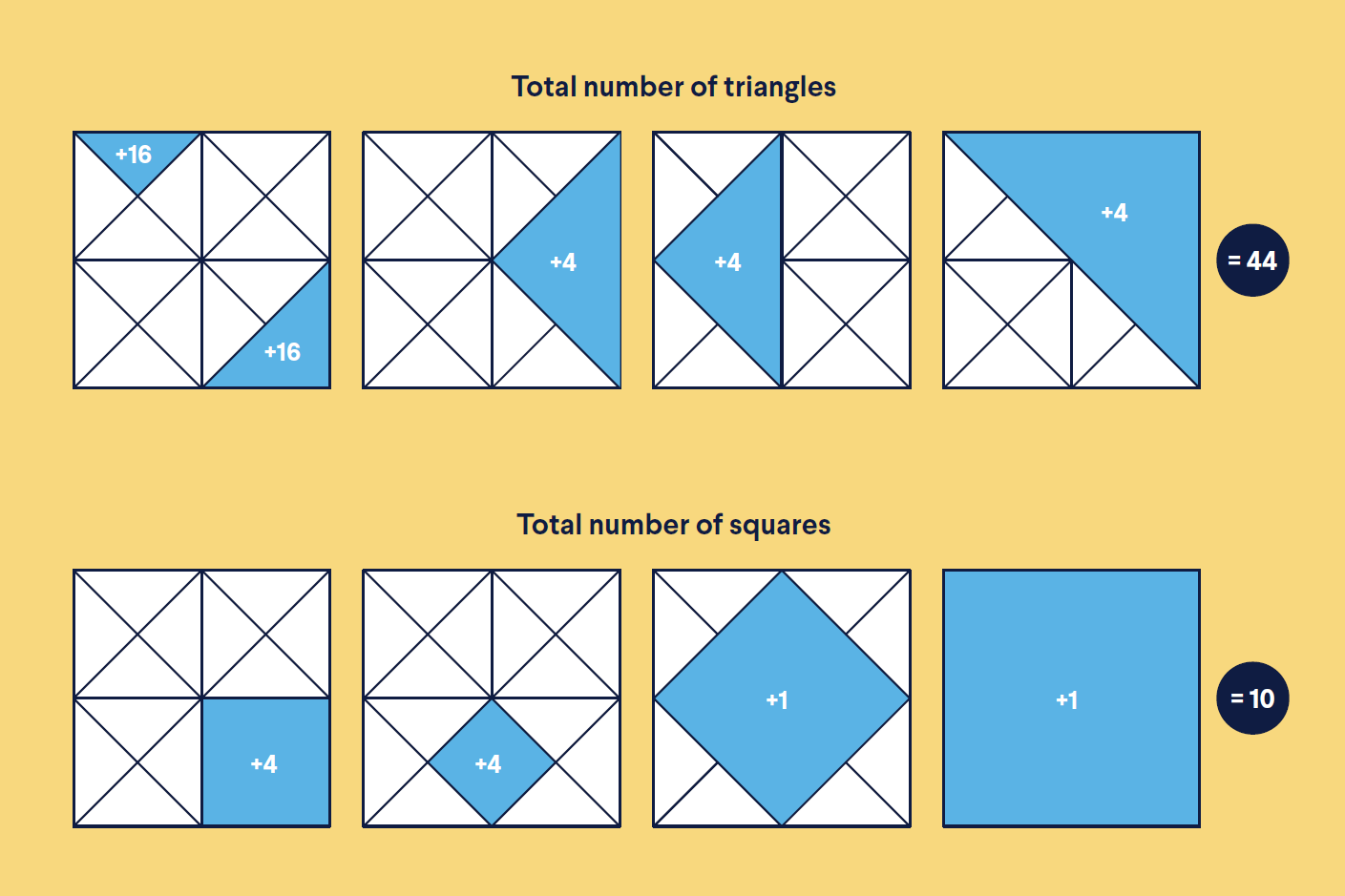
Hidden shapes
What is the total number of triangles and the total number of squares in the diagram? Look carefully, some may be hidden.

Answer