Year level: 6

Strand: Number

Lesson length: 75 mins

In this lesson, students are provided with a real-world problem related to shopping. The problem centres around gathering evidence to answer the question: ‘How does choosing sale items affect your grocery costs over a year?’ Introduce the 4-step problem-solving model to guide students to use mathematical modelling.

The intention of this lesson is for students to use mathematical modelling to solve the problem. It is suggested not to scaffold the problem so as to encourage students’ investigative thinking. It is preferable that students choose an appropriate mathematical operation and use computational thinking to break the problem into parts to help solve it. In the process, they may use several strategies to model and solve the problem. Ideally, you introduce the 4-step problem-solving model for students to follow in constructing their approach.

Mathematical modelling: Discounts Image

Achievement standard

Students use mathematical modelling to solve financial and other practical problems involving percentages and rational numbers, formulating and solving the problem, and justifying choices.

Content descriptions

Students use mathematical modelling to solve practical problems involving additive and multiplicative situations including financial contexts; formulate problems using number sentences and choose calculation strategies, using digital tools where appropriate; interpret and communicate solutions in terms of the situation. AC9M6N09

Students solve problems that require finding a familiar fraction, decimal or percentage of a quantity, including percentage discounts, choosing efficient calculation strategies and using digital tools where appropriate. AC9M6N07

General capabilities

Numeracy

Assess students' proficiency in working out a discount using a bar model to represent the saving.

  • Display the exit-ticket task:

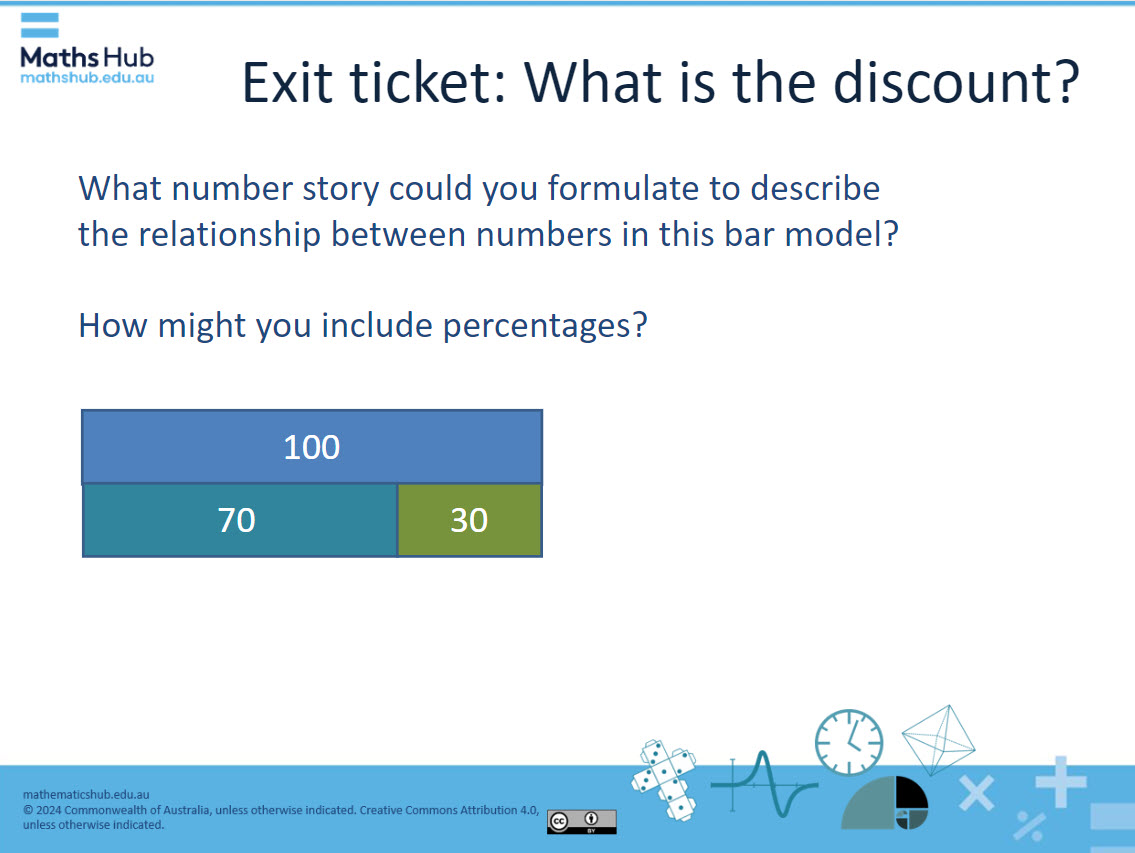
A slide of an exit ticket with a bar model of a rectangle labelled 100 and under it two smaller rectangles labelled 70 and the other 30.

In this task, students may suggest answers similar to:

  • The item cost $100. With a 30% discount, it cost $70.
  • The jumper costs $100, but with a 30% discount, you save $30 and pay $70.
  • The earbuds are priced at $100. With a 30% discount, you only pay $70.
  • You got a great deal buying something for $70 which originally cost $100 before the 30% sale.
  • Without the 30% sale you would have paid $100 instead of $70, so you saved $30.

Some students may:

  • need support to convert percentages into fractions or decimals, especially when determining the amount of the discount and the final price
  • confuse related terms such as ‘discount’, ‘percentage’ and ‘discounted price’.
  • be challenged to break down the problem into smaller parts and fully understand what mathematics is needed to solve the problem.

It is expected that students:

  • have an understanding of percentage and how to calculate the percentage of a given number
  • be familiar with multiplying and dividing numbers, as these skills are essential for calculating discounts
  • have a basic understanding of subtracting values to find the difference between original and discounted prices (savings)
  • be familiar with currency and the concept of pricing, including how to interpret item price and totals.

It is also assumed students are familiar with terms such as:

  • total
  • discount
  • percentage
  • discounted price
  • savings
  • price
  • daily, weekly, monthly, yearly.

What you need:

Learning goals

Learning intention

  • We are using the context of shopping and discounts to apply our knowledge of percentages.
  • We are using a 4-step problem-solving model to guide our thinking and to solve the problem.

Success criteria

By the end of this lesson, students can:

  • calculate percentage discounts on various shopping items
  • find the original price, sale price and savings using percentages
  • follow the 4-step problem-solving model to analyse and solve the problem using mathematical modelling.

Why are we learning about this?

We are learning about discounts to develop financial awareness and make smarter purchasing decisions. Understanding how discounts work helps us save money by identifying the best deals when shopping. This knowledge also helps us manage budgets effectively, ensuring we get the most value for our money. Being aware of discounts is an essential skill for making informed financial choices in everyday life.

Learning hook 10 mins

Use the teacher’s slides to introduce this part of the lesson.

Refer to slide 2 to introduce the task. Ask students: ‘What do you notice? What do you wonder?’ about the discounted offers and percentages displayed on the slide.

A slide with title What do you notice? What do you wonder? Underneath the text is 4 images of different types of sales, 10% off, buy one get one free, 25% and a bag with 50% off sale.

Slide 2

  • Use a classroom talk to generate discussion about discounts and percentages.
  • List what students notice or wonder, for example:
Notice Wonder
  • You often see these as discounts in stores.
  • 50% is the largest percentage and it means a half.
  • Three sales are percentages; buy-one-get-one-free is not.
  • The percentages are all different number amounts: 10, 25 and 50.
  • 25% is the same as one-quarter.
  • I wonder which sale saves the most money for different types of purchases?
  • I wonder how the buy-one-get-one-free deal compares to a percentage discount, such as 25% or 50% off?
  • I wonder what happens the more expensive the item on sale?

Check:

  • Do students understand the connection between percentages and their fraction equivalents, for example, 10% as one-tenth, 25% as one-quarter, 50% as one-half?
  • Can they model a buy-one-get-one-free scenario using a relevant example to work out the cost and the saving?

Explore 60 mins

Introduction (10 mins)

  • Review percentage and how to calculate it. Use the worked example on slide 3 to discuss each strategy with the students, so they can decide on their preferred approach. Present these four different calculation strategies, displaying each one with a mouse click. 

A slide with text: How would you work this out? Which calculation strategy do you prefer? In the centre of the slide is the text What is 50% of 10?Four ways to work out What is 50% of 10? are listed in 4 separate boxes Box 1: 50% is the same as ½.To find half of 10, divide 10 by 2. 10 ÷ 2 = 5. So, 50% of 10 is 5. Box 2: 50% can be written as the decimal 0.5. Multiply 10 by 0.5: 10 × 0.5 = 5. So, 50% of 10 is 5. Box 3: Break 10 into two equal parts. Half of 10 is: 5. So, 50% of 10 is 5. Box: 4 Partition the bar into two equal parts, as 50% means half.

Slide 3 with animation content revealed

A slide with title Impact of sales offers Underneath the text is 4 images of different types of sales in a table, In the first row labelled sales offer is 10% off, buy one get one free, 25% and a bag

Slide 4

Activity 1: Calculate discount and discounted price (10 mins)

Engage students in calculating the discount and discounted price using four discount offers. Using the item cost of $20.00, ask students to calculate the discount using their preferred calculation strategy. Refer to slides 4, 5 and 6.

  • 50% off: Discount is $10.00, discounted price is $10.00 (saving $10.00)
  • 10% off: Discount is $2.00, discounted price is $18.00 (saving $2.00)
  • 25% off: Discount is $5.00, discounted price is $15.00 (saving $5.00)
  • Buy-one-get-one-free: $20.00 (assuming you get two items for $20.00, so it feels like you're paying $10.00 per item)

Differentiation (support):

  • Can you represent $20 using physical materials such as counters? Choose one discount to calculate.
  • How much do you save (that is, what is the discount)? How much do you pay (that is, what is the discounted price)?
  • How might you use subtraction to calculate the discounted price?

Differentiation (extension):

  • Can you calculate the discounts and discounted price on a higher-priced item?
  • Can you calculate the discounted price in one step without the need to subtract the discount to get the discounted price? Here’s a clue: 10% of 100 is 10. 90% of 100 is 90. Can you see how this applies to calculating discounted prices more efficiently? For example, ‘Discounted price: $100.00 × (1 - 0.10) = $100.00 × 0.90 = $90.00’.

Activity 2: Using a 4-step problem solving process (40 mins)

Use slide 7 to introduce the problem, ‘How does choosing sale items affect your grocery costs over a year?’ Describe the shopping habits of two people.

A slide with the title Have you ever wondered? Under the title is the question How does choosing sale items affect your grocery costs over a year? Under this text are two icons; a sale icon next to another icon with the text buy and an arrow to represent online shopping. Under the sale icon is text: Marie shops for specials and waits for sale items. She always gets a bargain. Under Buy icon is text: Marco buys items as he needs them and usually doesn't wait for sales. At times, he finds an item on sale.A slide showing the four-step problem solving model. Text is Identify and describe with a globe with gears around it. Next is the word plan with puzzle pieces. Next is The text apply and do with mathematical symbols. Lastly Speech bubbles with text 'communicate'.

Slide 7 and Slide 10

Use slides 9 to 14 to introduce the 4-step problem-solving model.

STEP 1: What numbers or pieces of information do you need to represent the problem mathematically? (Slide 11)

STEP 2: Suggest possible approaches to consider in the plan stage. (Slide 12)

STEP 3: Apply calculation strategies to determine percentages. How might you calculate weekly, monthly and yearly savings? Solve the problem through a series of steps and create a visual representation of your mathematical solution. (Slide 13)

STEP 4: Share your solution. Explain why you chose your method of modelling the problem.

For those students familiar with using spreadsheets such as MS Excel, provide the spreadsheet Discounts xls. The interface shows how a simple formula can be used to automate calculating the discount and discounted price of an item discounted by a certain percentage. The spreadsheet then shows a table of groceries that can be used to create their own list and automate the discount and discounted price. Next, students could sum each column to calculate the total.

Differentiation (support)

  • How much might Marie save in a week if she brought 2 or 3 items from the list on sale? How much might she save over a month, which has 4 weeks? How much might she save in a year, which has 12 months? How could you represent that?

Differentiation (extension)

  • How much might Marie save compared to Marco if they both included all the items from the list? (Slide 8)
  • What percentage discount do you assume Marco might receive on his purchases (say, if 3 out of 10 of the items purchased are on sale)? Consider the percentage and justify your choice. What is the difference in cost per year? How can you show this?

Summary and reflection 5 mins

Summarise the lesson’s key points and invite students to reflect on what they’ve learned.

  • What did you learn about discounts and percentages?
  • What calculation strategy did you find most effective?
  • How do you think understanding percentages and discounts will help you in everyday life?